EE445S Real-Time Digital Signal Processing Laboratory
Handout I: Analog Sinusoidal Modulation Summary
Many ways exist to modulate a message signal 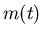 to produce a
modulated (transmitted) signal
to produce a
modulated (transmitted) signal 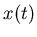 .
For amplitude, frequency, and phase modulation, modulated signals
can be expressed in the same form as
.
For amplitude, frequency, and phase modulation, modulated signals
can be expressed in the same form as
where 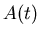 is a real-valued amplitude function (a.k.a. the envelope),
is a real-valued amplitude function (a.k.a. the envelope),
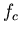 is the carrier frequency, and
is the carrier frequency, and
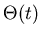 is the real-valued phase function.
Using this framework, several common modulation schemes are described below.
In the table below, the amplitude modulation methods are
double sideband larger carrier (DSB-LC),
DSB suppressed carrier (DSB-SC),
DSB variable carrier (DSB-VC), and
single sideband (SSB).
The hybrid amplitude-frequency modulation is quadrature amplitude
modulation (QAM).
The angle modulation methods are phase and frequency modulation.
is the real-valued phase function.
Using this framework, several common modulation schemes are described below.
In the table below, the amplitude modulation methods are
double sideband larger carrier (DSB-LC),
DSB suppressed carrier (DSB-SC),
DSB variable carrier (DSB-VC), and
single sideband (SSB).
The hybrid amplitude-frequency modulation is quadrature amplitude
modulation (QAM).
The angle modulation methods are phase and frequency modulation.
| Modulation |
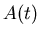 |
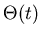 |
Carrier |
Type |
Use |
| DSB-LC |
![$A_c \left[ 1 + k_a m(t) \right]$](img7.gif) |
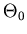 |
Yes |
Amplitude |
AM radio |
| DSB-SC |
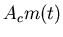 |
 |
No |
Amplitude |
|
| DSB-VC |
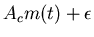 |
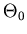 |
Yes |
Amplitude |
|
| SSB |
![$A_c \sqrt{m^2(t) + \left[ m(t) \star h(t) \right]^2}$](img11.gif) |
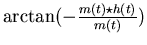 |
No |
Amplitude  |
Marine radios |
| QAM |
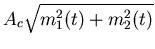 |
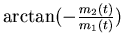 |
No |
Hybrid |
Satellite |
| Phase |
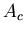 |
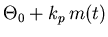 |
No |
Angle |
Underwater |
| |
|
|
|
|
modems |
| Frequency |
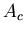 |
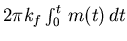 |
No |
Angle |
FM radio |
| |
|
|
|
|
TV audio |
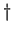
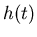 is the impulse response of a bandpass filter or phase
shifter to effect a cancellation of one pair of redundant sidebands.
For ideal filters and phase shifters, the modulation is amplitude modulation
because the phase would not carry any information about
is the impulse response of a bandpass filter or phase
shifter to effect a cancellation of one pair of redundant sidebands.
For ideal filters and phase shifters, the modulation is amplitude modulation
because the phase would not carry any information about 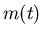 .
.
Each analog TV channel is allocated a bandwidth of 6 MHz.
The picture intensity and color information are transmitted using
vestigal sideband modulation.
Vestigal sideband modulation is a variant of amplitude modulation
(not shown above) in which the upper sideband is kept and a fraction of
the lower sideband is kept, or vice-versa.
In an analog TV signal, the audio portion is frequency modulated.
The following quantity is known as the complex envelope
where
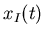 is called the in-phase component and
is called the in-phase component and
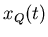 is called the quadrature component.
Both
is called the quadrature component.
Both 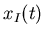 and
and 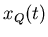 are lowpass signals, and hence,
the complex envelope
are lowpass signals, and hence,
the complex envelope 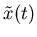 is a lowpass signal.
An alterative representation for the modulated signal
is a lowpass signal.
An alterative representation for the modulated signal 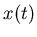 is
is
Brian L. Evans
![]() to produce a
modulated (transmitted) signal
to produce a
modulated (transmitted) signal ![]() .
For amplitude, frequency, and phase modulation, modulated signals
can be expressed in the same form as
.
For amplitude, frequency, and phase modulation, modulated signals
can be expressed in the same form as
![$A_c \sqrt{m^2(t) + \left[ m(t) \star h(t) \right]^2}$](img11.gif)