Introduction to Computation in Matlab

Prof. Brian L. Evans, Dept. of ECE, The University of Texas, Austin, Texas USA

Matlab's forte is numeric calculations with matrices and vectors. A vector can be defined as

vec = [1 2 3 4];

The first element of a vector is at index 1. Hence, vec(1) would return 1. The semicolon at the end of a Matlab command suppresses the printing of the result of an operation.

One can apply the same computation on each element of a vector. This is also known as pointwise, or point-by-point, calculation. For example, squaring each element of the vector vec

vec .^ 2

would give

[1 4 9 16]

One could compute the vector dot product (a.k.a. inner product) of vector vec with itself by

vec * vec'

which gives 30. The apostrophe operation denotes vector (or matrix) transposition.

As an example of defining and computing with matrices, the following lines would define a 2 x 3 matrix A, then define a 3 x 2 matrix B, and finally compute the matrix C that is the product of the two matrices A and B:

A = [1 2 3; 4 5 6]
B = [7 8; 9 10; 11 12]
C = A*B

Here is the resulting output from Matlab, which consists of one output per line of code because there is no semicolon at the end of each line to suppress the output:

A =
     1     2     3
     4     5     6

B =
     7     8
     9    10
    11    12

C =
    58    64
   139   154

We can plot signals by defining a set of time values and a set of signal amplitude values at those time values. For example, we can plot sine wave x(t) of frequency 1 Hz for one period (1 s) using a set of 101 points. The set of 101 points include 100 values from 0 s to 0.99 s, inclusive, plus the value at 1 s. This means that we are taking 100 samples/s:

t = 0 : 1/100 : 1;
x = sin(2*pi*t);
plot(t, x);

Here is the resulting plot:

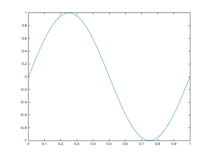
We can play a sinusoidal tone as a sound. Like we did to plot the sinusoidal signal above, we'll need choose how many samples per second to use. This is known as a sampling rate. An audio system supports a finite number of sampling rates— 8000 Hz is common. We'll play sinusoidal tone at 1000 Hz for 3 s at a sampling rate of 8000 Hz:

samplingRate = 8000;
t = 0 : 1/samplingRate : 3;
toneFreq = 1000;
x = sin(2*pi*toneFreq*t);
sound(x, fs);

Matlab Tutorials, Help and Training

Here are excellent Matlab tutorials:

https://stat.utexas.edu/training/software-tutorials#matlab

http://www.mathworks.com/academia/student_center/tutorials/mltutorial_launchpad.html

The following Matlab tutorial book is a useful reference:

Duane Hanselman and Bruce Littlefield, Mastering MATLAB, ISBN 9780136013303, 2011.

A full version of Matlab is available for your personal computers via a university site license:

http://www.ece.utexas.edu/it/matlab

Although the first few computer homework assignments will help step you through Matlab, it is strongly suggested that you take the free short courses that the Department of Statistics and Data Sciences will be offering. The schedule of those courses is available online at

https://stat.utexas.edu/training/software-short-courses

Technical support is provided through free consulting services from the Department of Statistics and Data Sciences. Simple queries can be e-mailed to stat.consulting@austin.utexas.edu. For more complicated inquiries, please go in person to their offices located in GDC 7.404. You can walk in or schedule an appointment online.