Instructions:
You are encouraged to work on the problem set in groups and turn in one problem set for the entire group. Remember to put all your names on the solution sheet. Also remember to put the name of the TA in whose discussion section you would like the problem set returned to you.

1. During lecture, we discussed Tomasulo's algorithm. We also briefly discussed the concepts of "data flow" and "data flow graph". The concept of data flow is that an instruction gets executed when its input data (both its source operands) are available. We can represent the computation of the program using a directed graph called the "data flow graph". Nodes of the data flow graph are instructions. Arcs of the graph show the flow dependencies between instructions. In class, Professor Patt mentioned that Tomasulo's algorithm forms the data flow graph for a program while that program is being executed.

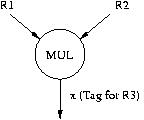
   Draw the dataflow graph for the code we used in lecture to describe Tomasulo's algorithm. Label the nodes with the opcodes of the instructions and the arcs with the tags. The program and the first node of the data flow graph are shown below.

      MUL  R1, R2, R3
      ADD  R3, R4, R5
      ADD  R2, R6, R7
      ADD  R9, R8, R10
      MUL  R7, R10, R11
      ADD  R5, R11, R5
   

   
2. Given the following code segment:

   for(i = 0; i < 100; i++)
     A[i] = (B[i] * C[i] + D[i]) / 2;
   

   Write Cray-like assembly code to perform the calculation. Then compute the number of cycles required for the code segment to execute on the following machines:
   1. Scalar processor
   2. Vector processor without chaining, 1 port to memory (1 load or store / cycle)
   3. Vector processor with chaining, 1 port to memory
   4. Vector processor with chaining, 2 read ports and 1 write port to memory
   Assume each machine has vector registers of length 64. The Multiply, Add, and Load units are pipelined and take 6, 4, and 11 cycles, respectively, to complete one operation. Memory is 16-way interleaved.
3. In lecture, Professor Patt discussed a 2-stage pipelined machine with delayed branches and a single-cycle delay slot.

   Show what the pipeline looks like and how the following code gets executed for four cases (based on taken, not-taken result of the conditional branch instructions).

    
               A
               B
               C 
   	    BC X
   	    BC Y
   	    D
   	    E
   	    F
   	    G
   	X   H 
   	Y   I 
   	    J
   

4. Suppose we have the following loop executing on a pipelined LC-3b machine.

            
   DOIT     STW   R1, R6, #0
            ADD   R6, R6, #1
            AND   R3, R1, R2
            BRz   EVEN
            ADD   R1, R1, #3
            ADD   R5, R5, #-1
            BRp   DOIT
   EVEN     ADD   R1, R1, #1
            ADD   R7, R7, #-1 
            BRp   DOIT
   

   
   Assume that before the loop starts, the registers are initialized to the following integer values:
   R1 <- 0
   R2 <- 1
   R5 <- 5
   R6 <- 4000
   R7 <- 5

   "Fetch" takes 1 cycle, "Decode" takes 1 cycle, "Execute" stage takes variable number of cycles depending on the type of instruction (see below), and "Store Result" stage takes 1 cycle.
   
   All execution units (including the load/store unit) are fully pipelined and the following instructions that use these units take the indicated number of cycles:
   
   STW: 3 cycles
   ADD: 3 cycles
   AND: 2 cycles
   BR : 1 cycle

   For example, the execution of an ADD instruction followed by a BR would look like:

   ADD       F | D | E1 | E2 | E3 | ST
   BR            F | D  | -  | -  | E1  | ST
   TARGET                                 F  | D
   

   This figure shows several things about the structure of the pipeline:

   • Whenever possible, data forwarding is used. Instructions that are dependent on the previous instructions can make use of the results produced before right after the previous instruction finishes the "Execute" stage.
   • Branch instructions require 1 "execute" cycle to resolve the branch. Hence, the target instruction can be fetched when the BR instruction is in ST stage.

   Also, you are given the following information about the pipeline and the ISA:

   • The pipeline implements "in-order execution". A scoreboarding scheme is used as discussed in class.
   • The pipeline emulates the LC-3b ISA. Hence, the above instructions are all LC-3b instructions.

   Answer the following questions:

   a) How many cycles does the loop above take to execute if no branch prediction is used?

   b) Suppose that a static BTFN (backward taken-forward not taken) branch prediction scheme is used to predict branches.

   i. How many cycles does the above loop take to execute with this scheme?

   ii. What is the branch prediction accuracy?

   iii. What is the prediction accuracy for each branch?

   c) Suppose that two-bit saturating up/down counters (as discussed in lecture) are used for branch prediction. Each branch instruction has its own counter. The counters are initialized to '10' state. Top bit of the counter is used as the prediction. Hence, the first time a branch is seen it will be predicted taken.

   i. How many cycles does the above loop take to execute if two-bit counters are used for branch prediction?

   ii. What is the branch prediction accuracy?

   iii. What is the prediction accuracy for each branch?

5. From Tanenbaum, 4th edition, Appendix A, 10.

   Signed decimal numbers consisting of n digits can be represented in n + 1 digits without a sign. Positive numbers have 0 as the leftmost digit. Negative numbers are formed by subtracting each digit from 9. Thus the negative of 014725 is 985274. Such numbers are called nine's complement numbers and are analogous to one's complement binary numbers. Express the following as three-digit nine's complement numbers: 6, -2, 100, -14, -1, 0.

6. From Tanenbaum, 4th edition, Appendix B, 4.

   The following binary floating-point number consists of a sign bit, an excess 63, radix 2 exponent, and a 16-bit fraction. Express the value of this number as a decimal number.

   0 0111111 0000001111111111

7. From Tanenbaum, 4th edition, Appendix B, 5.

   To add two floating point numbers, you must adjust the exponents (by shifting the fraction) to make them the same. Then you can add the fractions and normalize the result, if need be. Add the single precision IEEE floating-point numbers 3EE00000H and 3D800000H and express the normalized result in hexadecimal. ['H' is a notation indicating these numbers are in hexadecimal]

8. From Tanenbaum, 4th edition, Appendix B, 6.

   The Tightwad Computer Company has decided to come out with a machine having 16-bit floating-point numbers. The model 0.001 has a floating-point format with a sign bit, 7-bit, excess 63 exponent and 8-bit fraction. Model 0.002 has a sign bit, 5-bit, excess 15 exponent and a 10-bit fraction. Both use radix 2 exponentiation. What are the smallest and largest positive normalized numbers on both models? About how many decimal digits of precision does each have? Would you buy either one?

9. Write an LC-3b assembly program to add two 32-bit integers stored at memory locations x4000 and x4004. Your program should store the result at memory location x4008. We show below the layout of data in memory:

   x4000: Low 16 bits of first integer
   x4002: High 16 bits of first integer
   x4004: Low 16 bits of second integer
   x4006: High 16 bits of second integer
   x4008: Low 16 bits of the result
   x400A: High 16 bits of the result

   How many cycles does your program take to execute if the 32-bit integer at location x4000 is xFFFFFFFF and the 32-bit integer at location x4004 is x00000001?

10. Repeat the previous question assuming that the enhanced LC-3b ISA, which provides the following features:

    a. A 1-bit carry condition code (C). This condition code is set to 1 if the ADD operation generates a carry-out.
    b. A new instruction in the instruction set:

    ADDC DR, SR1, SR2/imm5

    which adds the contents of SR1 and SR2/imm5 together with the carry condition code to generate the sum in DR. ADDC instruction also sets the C condition code.

    How many cycles does your program take to execute if the 32-bit integer at location x4000 is xFFFFFFFF and the 32-bit integer at location x4004 is x00000001? Assume that ADDC instruction takes the same number of cycles as the ADD instruction to execute.