Instructions:
You are encouraged to work on the problem set in groups and turn in one problem set for the entire group. Remember to put all your names on the solution sheet. Also, remember to put the name of the TA and the time for the discussion section you would like the problem set turned back to you. Show your work.

1. (Adapted from 2.37 in textbook, and from Problem Set 1)
   Two 4-bit 2's complement numbers, n and m, are added, yielding s, the 4-bit result. Determine, using only the AND, OR, and NOT logical operations, if an overflow has occurred during the addition? Construct a logic circuit that does this. The inputs to the logic circuit are n[3:0], m[3:0], and s[3:0]. The output is 0 if no overflow occurs and 1 if an overflow does occur.
   
   
2. (2.54, and from Problem Set 1)
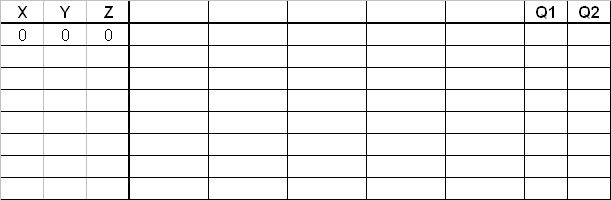
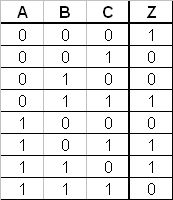
   Fill in the truth table for the equations given. The first line is done as an example. We have intentionally left several blank output columns for you to use as you wish.
   
   Q1 = NOT (NOT(X) OR (X AND Y AND Z))
   Q2 = NOT ((Y OR Z) AND (X AND Y AND Z))
   
   
   
   
3. (2.40)
   Write the decimal equivalents for these IEEE floating point numbers
   1. 0 10000000 00000000000000000000000
   2. 1 10000011 00010000000000000000000
   3. 0 11111111 00000000000000000000000
   4. 1 10000000 10010000000000000000000
   
   
4. (3.7)
   (Please refer to the figure for problem 3.7 on page 84 of the book) The circuit has a major flaw. Can you identify it? Hint: Evaluate the circuit for all sets of inputs.
   
   
5. Fill in the truth table for the logical expression OUT = NOT(NOT(A) AND NOT(B) AND NOT(C)). What single logic gate has this same truth table?
   
   
   
   
6. (3.11)
   
   1. Draw a transistor-level diagram for a three-input AND gate and a three-input OR gate. Do this by extending the designs from Figures 3.6a and 3.7a. (These figures can be found in the book on pages 56 & 57 respectively).
      
   2. Replace the transistors in your diagrams from part (a) with either a wire or no wire to reflect the circuit’s operation when the following inputs are applied:
      1. A = 1, B = 0, C = 0
      2. A = 0, B = 0, C = 0
      3. A = 1, B = 1, C = 1
   
   
7. (Adapted from 3.13)
   
   1. How many output lines will a five-input decoder have?
   2. How many output lines will an eight-input decoder have?
   3. How many output lines will an n-input decoder have? (n can be any number)
   
   
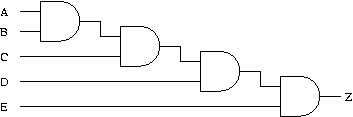
8. Suppose we wanted to build a 5-input AND gate, but we only had 2-input AND gates available. Since AND is an associative logical operator, Z = A AND B AND C AND D AND E could be computed as Z = ((((A AND B) AND C) AND D) AND E), as shown below in Figure 1.
   
   
   Figure 1
   
   It turns out that XOR is also an associative logical operator, and a 5-input XOR gate can be constructed using 2-input XOR gates in the same manner (see Figure 2 below).
   
   
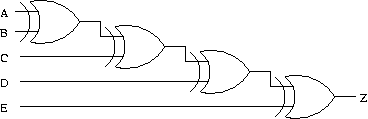
   Figure 2
   
   
   1. Complete a truth table for the gate-level logic circuit shown in Figure 2 above.
   2. What do you notice about the input combinations that give an output value of 1? What do you notice about the input combinations that give an output value of 0?
   
   
9. (3.16)
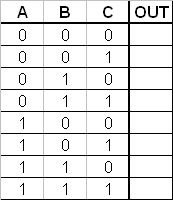
   Given the following truth table, generate the gate-level logic circuit, using the implementation algorithm referred to in Section 3.3.4.
   
   
   
   
10. (3.19)
    Logic circuit 1 in Figure 3.36 (page 87 of the book) has inputs A, B, C. Logic circuit 2 in Figure 3.37 (page 87 of the book) has inputs A and B. Both logic circuits have an output D. There is a fundamental difference between the behavioral characteristics of these two circuits. What is it? Hint: What happens when the voltage at input A goes from 0 to 1 in both circuits?
    
    
11. (Adapted from 3.22)
    Implement a 4-to-1 mux using only 2-to-1 muxes making sure to properly connect all of the terminals. Remember that you will have 4 inputs (A, B, C, and D), 2 control signals (S1 and S0), and 1 output (OUT). After implementing the 4-1 mux, fill in the truth table below.
    
    



12. (3.24)
    
    1. Figure 3.39 (page 89 of the book) shows a logic circuit that appears in many of today’s processors. Each of the boxes is a full-adder circuit. What does the value on the wire X do? That is, what is the difference in the output of this circuit if X = 0 versus if X = 1?
    2. Construct a logic diagram that implements an adder/subtracter. That is, the logic circuit will compute A + B or A – B depending on the value of X. Hint: Use the logic diagram of Figure 3.39 as a building block.