Determine the decimal value of the following IEEE floating point numbers.
1 10000000 101000000000000000000000 00000000 010100000000000000000001 11111111 00000000000000000000000
Using a residue number system with two moduli, represent all of the decimal values between 0 and 11 inclusive when the moduli are
- 4 and 3
- 6 and 2
Using the Booth Multiplication Algorithm, multiply the two unsigned 10-bit numbers 0011011110 and 0001110010. Show the intermediate results after each step.
From Tanenbaum, 4th edition, Appendix B, 4.
The following binary floating-point number consists of a sign bit, an excess 63, radix 2 exponent, and a 16-bit fraction. Express the value of this number as a decimal number.
0 0111111 0000001111111111
From Tanenbaum, 4th edition, Appendix B, 5.
To add two floating point numbers, you must adjust the exponents (by shifting the fraction) to make them the same. Then you can add the fractions and normalize the result, if need be. Add the single precision IEEE floating-point numbers 3EE00000H and 3D800000H and express the normalized result in hexadecimal. ['H' is a notation indicating these numbers are in hexadecimal]
From Tanenbaum, 4th edition, Appendix B, 6.
The Tightwad Computer Company has decided to come out with a machine having 16-bit floating-point numbers. The model 0.001 has a floating-point format with a sign bit, 7-bit, excess 63 exponent and 8-bit fraction. Model 0.002 has a sign bit, 5-bit, excess 15 exponent and a 10-bit fraction. Both use radix 2 exponentiation. What are the smallest and largest positive normalized numbers on both models? About how many decimal digits of precision does each have? Would you buy either one?
The following numbers are represented exactly with a 9-bit floating point representation, in the format of the IEEE Floating Point standard:
-infinity, -1, 0, 5/16, 19.5, 48.
- How many bits are needed for the fraction?
- What is the bias?
- Write each number in in the 9-bit floating point representation,
below:
Value Representation 48 19.5 5/16 0 -1 -infinity
In class, we discussed how to use Booth's algorithm to be able to multiply 2 bits in a cycle. Implement the same technique to multiply 4 bits in a cycle. Note that since the algorithm can only do one add (or subtract) in one cycle, that goal cannot be achieved. i.e. sometimes, we can only process 2 or 3 bits in 1 cycle. If the multiplier number is random, on average how many bits are processed at each cycle?
Given the following code:
MUL R3, R1, R2
ADD R5, R4, R3
ADD R6, R4, R1
MUL R7, R8, R9
ADD R4, R3, R7
MUL R10, R5, R6Note: Each instruction is specified with the destination register first.
Calculate the number of cycles it takes to execute the given code on the following models:
- A non-pipelined machine.
- A pipelined machine with scoreboarding and five adders and five multipliers.
- A pipelined machine with scoreboarding and one adder and one multiplier.
Note: For all machine models, use the basic instruction cycle as follows:
- Fetch (one clock cycle)
- Decode (one clock cycle)
- Execute (MUL takes 6, ADD takes 4 clock cycles). The multiplier and the adder are not pipelined.
- Write-back (one clock cycle)
Do not forget to list any assumptions you make about the pipeline structure (e.g., data forwarding between pipeline stages). Infact, we encourage you to solve the above mentioned questions with data forwarding as well, but, you are not required to do so.
Suppose we have the following loop executing on a pipelined LC-3b machine.
DOIT STW R1, R6, #0
ADD R6, R6, #2
AND R3, R1, R2
BRz EVEN
ADD R1, R1, #3
ADD R5, R5, #-1
BRp DOIT
EVEN ADD R1, R1, #1
ADD R7, R7, #-1
BRp DOITAssume that before the loop starts, the registers have the following decimal values stored in them:
| Register | Value |
|---|---|
| R0 | 0 |
| R1 | 0 |
| R2 | 1 |
| R3 | 0 |
| R4 | 0 |
| R5 | 5 |
| R6 | 4000 |
| R7 | 5 |
The fetch stage takes one cycle, the decode stage also takes one cycle, the execute stage takes a variable number of cycles depending on the type of instruction (see below), and the store stage takes one cycle.
All execution units (including the load/store unit) are fully pipelined and the following instructions that use these units take the indicated number of cycles:
| Instruction | Number of Cycles |
|---|---|
| STW | 3 |
| ADD | 3 |
| AND | 2 |
| BR | 1 |
Data forwarding is used wherever possible. Instructions that are dependent on the previous instructions can make use of the results produced right after the previous instruction finishes the execute stage. Multiple Instructions can write the results to the register file concurrently in the same cycle. (Text updated 11/11/16)
The target instruction after a branch can be fetched when the BR instruction is in ST stage. For example, the execution of an ADD instruction followed by a BR would look like:
ADD F | D | E1 | E2 | E3 | ST BR F | D | - | - | E1 | ST TARGET F | D
The pipeline implements “in-order execution.” A scoreboarding scheme is used as discussed in class.
Answer the following questions:
How many cycles does the above loop take to execute if no branch prediction is used?
How many cycles does the above loop take to execute if all branches are predicted with 100% accuracy.
How many cycles does the above loop take to execute if a static BTFN (backward taken-forward not taken) branch prediction scheme is used to predict branch directions? What is the overall branch prediction accuracy? What is the prediction accuracy for each branch?
A five instruction sequence executes according to Tomasulo's
algorithm. Each instruction is of the form ADD DR,SR1,SR2 or MUL
DR,SR1,SR2. ADDs are pipelined and take 9 cycles
(F-D-E1-E2-E3-E4-E5-E6-WB). MULs are also pipelined and take 11 cycles (two
extra execute stages). The microengine must wait until a result is in
a register before it sources it (reads it as a source operand).
The register file before and after the sequence are shown below (tags for “After” are ignored).
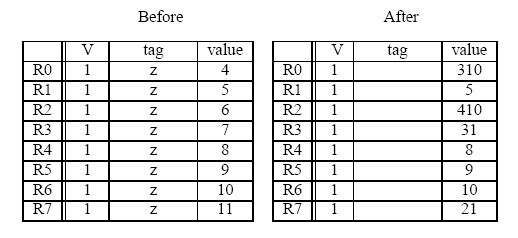
-
Complete the five instruction sequence in program order in the space below. Note that we have helped you by giving you the opcode and two source operand addresses for instruction 4. (The program sequence is unique.)
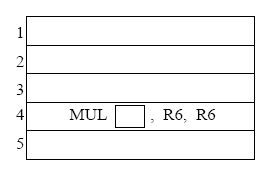
-
In cycle 1 instruction 1 is fetched. In cycle 2, instruction 1 is decoded and instruction 2 is fetched. In cycle 3, instruction 1 starts execution, instruction 2 is decoded, and instruction 3 is fetched.
Assume the reservation stations are all initially empty. Put each instruction into the next available reservation station. For example, the first ADD goes into “a”. The first MUL goes into “x”. Instructions remain in the reservation stations until they are completed. Show the state of the reservation stations at the end of cycle 8.
Note: to make it easier for the grader, when allocating source registers to reservation stations, please always have the higher numbered register be assigned to SR2.
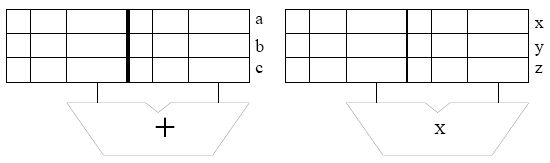
-
Show the state of the Register Alias Table (V, tag, Value) at the end of cycle 8.
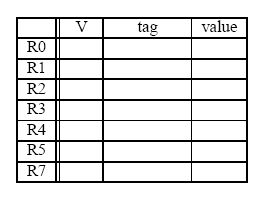
Consider the following piece of code:
for(i = 0; i < 100; i++)
A[i] = ((B[i] * C[i]) + D[i]) / 2;Translate this code into assembly language using the following instructions in the ISA (note the number of cycles each instruction takes is shown with each instruction):
Opcode Operands Number of Cycles Description LEARi, X1 Ri ← address of X LDRi, Rj, Rk11 Ri ← MEM[Rj + Rk] STRi, Rj, Rk11 MEM[Rj + Rk] ← Ri MOVIRi, Imm1 Ri ← Imm MULRi, Rj, Rk6 Ri ← Rj × Rk ADDRi, Rj, Rk4 Ri ← Rj + Rk ADDRi, Rj, Imm4 Ri ← Rj + Imm RSHFARi, Rj, amount1 Ri ← RSHFA (Rj, amount) BRccX1 Branch to X based on condition codes Assume it takes one memory location to store each element of the array. Also assume that there are 8 registers (R0-R7).
How many cycles does it take to execute the program?
-
Now write Cray-like vector/assembly code to perform this operation in the shortest time possible. Assume that there are 8 vector registers and the length of each vector register is 64. Use the following instructions in the vector ISA:
Opcode Operands Number of Cycles Description LDVst, #n1 Vst ← n LDVln, #n1 Vln ← n VLDVi, X + offset11, pipelined VSTVi, X + offset11, pipelined VmulVi, Vj, Vk6, pipelined VaddVi, Vj, Vk4, pipelined VrshfaVi, Vj, amount1 How many cycles does it take to execute the program on the following processors? Assume that memory is 16-way interleaved.
- Vector processor without chaining, 1 port to memory (1 load or store per cycle)
- Vector processor with chaining, 1 port to memory
- Vector processor with chaining, 2 read ports and 1 write port to memory
Little Computer Inc. is now planning to build a new computer that is more suited for scientific applications. LC-3b can be modified for such applications by replacing the data type Byte with Vector. The new computer will be called LmmVC-3 (Little 'mickey mouse' Vector Computer 3). Your job is to help us implement the datapath for LmmVC-3. LmmVC-3 ISA will support all the scalar operations that LC-3b currently supports except the LDB and STB will be replaced with VLD and VST respectively. Our datapath will need to support the following new instructions:

Note: VDR means “Vector Destination Register” and VSR means “Vector Source Register.”
- MOVI
- If IR[11:9] = 000, MOVI moves the unsigned quantity amount6 to Vector Stride Register (Vstride). If IR[11:9] = 001, MOVI moves the unsigned quantity amount6 to Vector Length Register (Vlength). This instruction has already been implemented for you.
- VLD
- VLD loads a vector of length Vlength from memory into VDR. VLD uses the opcode previously used by LDB. The starting address of the vector is computed by adding the LSHF1(SEXT(offset6)) to BaseR. Subsequent addresses are obtained by adding LSHF1(ZEXT(Vstride)) to the address of the preceding vector element.
- VST
- VST writes the contents of VSR into memory. VST uses the opcode previously used by STB. Address calculation is done in the same way as for VLD.
- VADD
- If IR[4] is a 1, VADD adds two vector registers (VSR1 and VSR2) and stores the result in VDR. If IR[4] is a 0, VADD adds a scalar register (SR2) to every element of VSR and stores the result in VDR.
VLD, VST, and VADD do not modify the content of Vstride and Vlength registers.
The following five hardware structures have been added to LC-3b in order to implement LmmVC-3.
- Vector Register File with eight 63-element Vector registers
- Vector Length Register
- Vector Stride Register
- A third input to DRMUX containing IR[8:6]
- Grey box A
- Box labeled X
These structures are shown in the LmmVC-3 datapath diagram:
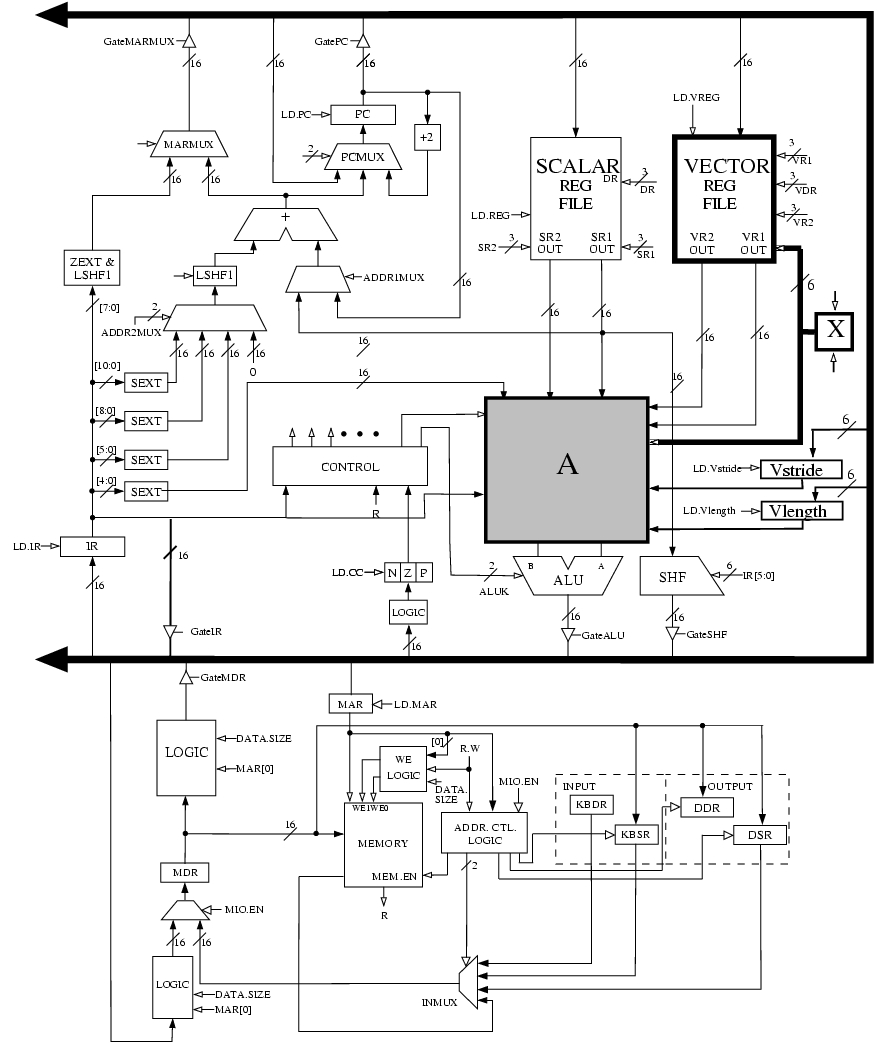
A 6-bit input to the Vector Register file has been labeled X on the datapath diagram. What is the purpose of this input? (Answer in less than 10 words )
The logic structure X contains a 6-bit register and some additional logic. X has two control signals as its inputs. What are these signals used for?
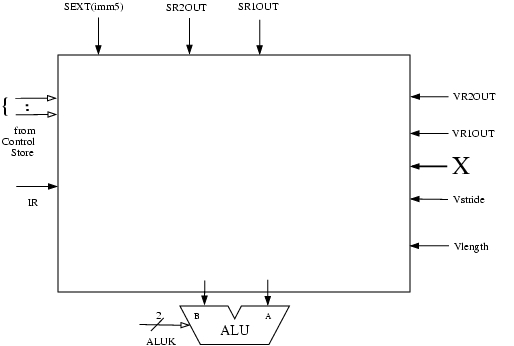
Grey box A contains several additional muxes on both input lines to the ALU. Complete the logic diagram of grey box A (shown below) by showing all muxes and interconnects. You will need to add new signals to the control store; be sure to clearly label them in the logic diagram.
- Keep in mind that we will still need to support all the existing scalar operations.
- The XOR operation in the ALU can be used to compare two values.
- Our solution required 3 additional control signals and 6 2-to-1 muxes.
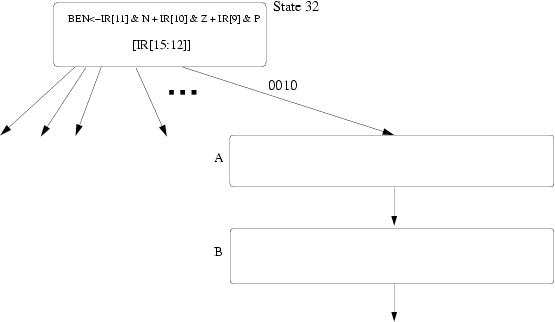
-
We show the beginning of the state diagram necessary to implement VLD. Using the notation of the LC-3b State Diagram, add the states you need to implement VLD. Inside each state describe what happens in that state. You can assume that you are allowed to make any changes to the microsequencer that you find necessary. You do not have to make/show these changes. You can modify BaseR and the condition codes. Make sure your design works when Vlength equals 0. Full credit will be awarded to solutions that require no more than 7 states.
The following data flow graph receives as inputs a value x, an n element vector V0, V1, ..., Vn-1, the value n, and a value 0 on its four input ports.

What "answer" is produced by the execution of this data flow graph?
We must compute the following expression:
a*x^6 + b*x^5 + c*x^4 + d*x^3 + e*x^2 + f*x + g
- How many operations and time-steps will the computation take on a single processor system (Use the smallest number of operations possible)?
- How many operations and time-steps will the computation take on a multiprocessor system with 4 processors? (Use the smallest number of operations possible)
- What is the speedup of the multiprocessor system over a single processor?
Speed-up with p processors is defined as T1/Tp, where T1 is the time to solve the problem with one processor and Tp is the time to solve the problem if you have p processors. What important requirement is there on T1?