EE 306 - Problem Set 3

Department of Electrical and Computer Engineering

The University of Texas at Austin

EE 306, Fall 2017
Problem Set 3
Due: October 16th at 3:30pm<(due date updated on 10/04/17)br> Yale N. Patt, Instructor
TAs: Stephen Pruett, Siavash Zangeneh, Aniket Deshmukh, Zachary Susskind, Meiling Tang, Jiahan Liu

Instructions:
You are encouraged to work on the problem set in groups and turn in one problem set for the entire group. Remember to put all your names on the solution sheet. Also, remember to put the name of the TA and the time for the discussion section you would like the problem set turned back to you. Show your work.

  1. Moved from Problem Set 2
    A logic circuit consisting of 6 gated D latches and 1 inverter is shown below:


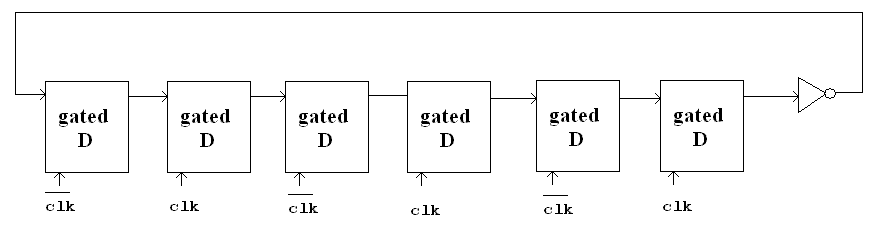
    Figure 5

    Figure
    Figure 6

    Let the state of the circuit be defined by the state of the 6 D latches. Assume initially the state is 000000 and clk starts at the point labeled t0.
    Question: What is the state after 50 cyles. How many cycles does it take for a specific state to show up again?

  2. We want to make a state machine for the scoreboard of the Texas vs. Oklahoma Football game. The following information is required to determine the state of the game:

    1. Score: 0 to 99 points for each team
    2. Down: 1, 2, 3, or 4
    3. Yards to gain: 0 to 99
    4. Quarter: 1, 2, 3, 4
    5. Yardline: any number from Home 0 to Home 49, Visitor 0 to Visitor 49, 50
    6. Possesion: Home, Visitor
    7. Time remaining: any number from 0:00 to 15:00, where m:s (minutes, seconds)
    (a) What is the minimum number of bits that we need to use to store the state required?
    (b) Suppose we make a separate logic circuit for each of the seven elements on the scoreboard, how many bits would it then take to store the state of the scoreboard?
    (c) Why might the method of part b be a better way to specify the state than the method of part a?

  3. Shown below is a partially completed state diagram of a finite state machine that takes an input string of H (heads) ant T (tails) and produces an output of 1 every time the string HTHH occurs.

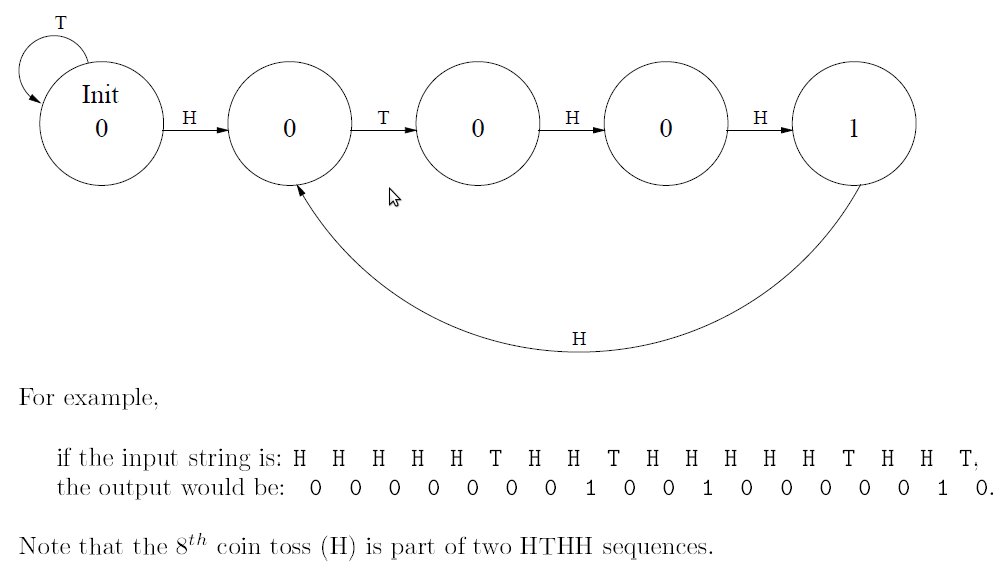
    Figure 4
    1. Complete the state diagram of the finite state machine that will do this for any input sequence of any length
    2. If this state machine is implemented with a sequential logic circuit how many state variables will be needed?

  4. (3.31)
    If a particular computer has 8 byte addressability and a 4 bit address space, how many bytes of memory does that computer have?

  5. Elevator Problem Revisited
    Recall the elevator controller problem on Problem Set 2. You were asked to design the truth table for an elevator controller such that the option to move up or down by one floor is disabled. If there is a request to move only one floor or to move zero floors, the elevator should remain on the current floor. For this problem, you will design the state machine for the sequential logic circuit for an elevator controller which performs the same operation. You can assume that the building the elevator is in has 4 floors. The input to the state machine is the next requested floor. There will be a state for each floor the elevator could be on. Draw a finite state machine that describes the behavior of the elevator controller. How many bits are needed for the inputs?

  6. (3.33)
    Using Figure 3.21 on page 69 in the book, the diagram of the, 22-by-3-bit memory.
    1. To read from the fourth memory location, what must the values of A[1:0] and WE be?
    2. To change the number of locations in the memory from 4 to 60, how many address lines would be needed? What would the addressability of the memory be after this change was made?
    3. Suppose the width (in bits) of the program counter is the minimum number of bits needed to address all 60 locations in our memory from part (b). How many additional memory locations could be added to this memory without having to alter the width of the program counter?

7.     The figure below is a diagram of a 22-by-16-bit memory, similar in implementation to the memory of Figure 3.21 in the textbook. Note that in this figure, every memory cell represents 4 bits of storage instead of 1 bit of storage. This can be accomplished by using 4 Gated-D Latches for each memory cell instead of using a single Gated-D Latch. The hex digit inside each memory cell represents what that cell is storing prior to this problem.



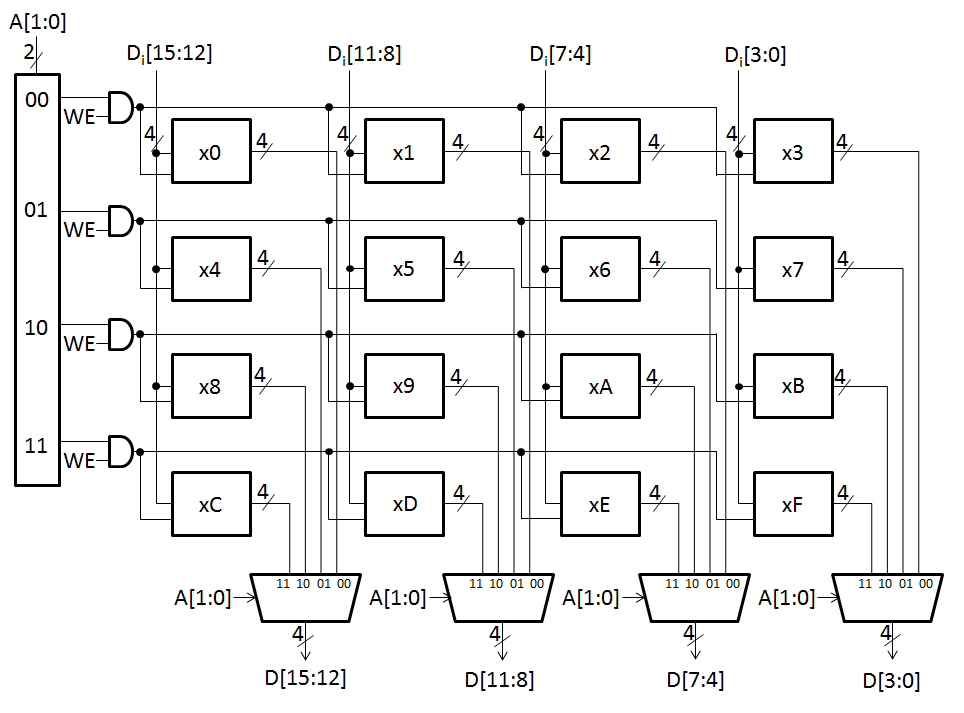
Figure 3: 22-by-16 bit memory

    1. What is the address space of this memory?
    2. What is the addressability of this memory?
    3. What is the total size in bytes of this memory?
    4. This memory is accessed during four consecutive clock cycles. The following table lists the values of some important variables just before the end of the cycle for each access. Each row in the table corresponds to a memory access. The read/write column indicates the type of access: whether the access is reading memory or writing to memory. Complete the missing entries in the table.

WE

A[1:0]

Di[15:0]

D[15:0]

Read/Write

0

01

xFADE

1

10

xDEAD

xBEEF

x0123

Read

11

xFEED

Write

8.     (3.41)
The Eta Kappa Nu (HKN) office sells sodas for 35 cents. Suppose they install a soda controller that only takes the following three inputs: nickel, dime, and quarter. After you put in each coin, you push a pushbutton to register the coin. If at least 35 cents has been put in the controller, it will output a soda and proper change (if applicable). Draw a finite state machine that describes the behavior of the soda controller. Each state will represent how much money has been put in (Hint: There will be seven of those states). Once enough money has been put in it, the controller will go to a final state where the person will receive a soda and proper change (Hint: There are five such final states). From the final state, the next coin that is put in will start the process again, contributing to the next purchase.

 

  1. Suppose that an instruction cycle of the LC-3 has just finished and another one is about to begin. The following table describes the values in select LC-3 registers and memory locations:

Register

Value

IR

x3001

PC

x3003

R0

x3000

R1

x3000

R2

x3002

R3

x3000

R4

x3000

R5

x3000

R6

x3000

R7

x3000

Memory Location

Value

x3000

x62BF

x3001

x3000

x3002

x3001

x3003

x62BE

For each phase of the new instruction cycle, specify the values that PC, IR, MAR, MDR, R1, and R2 will have at the end of the phase in the following table:

PC

IR

MAR

MDR

R0

R1

R2

R3

R4

R5

R6

R7

Fetch

Decode

Evaluate Address

Fetch Operands

Execute

Store Result

Hint: Example 4.2 on page 104 illustrates the LDR instruction of the LC-3. Notice that values of memory locations x3000, and 3003 can be interpreted as LDR instructions.

  1. (4.8)
    Suppose a 32-bit instruction has the following format:

    OPCODE

    DR

    SR1

    SR2

    UNUSED

    If there are 255 opcodes and 120 registers, and every register is available as a source or destination for every opcode,

    1. What is the minimum number of bits required to represent the OPCODE?
    2. What is the minimum number of bits required to represent the Destination Register (DR)?
    3. What is the maximum number of UNUSED bits in the instruction encoding?

  2. A State Diagam
    We wish to invent a two-person game, which we will call XandY that can be played on the computer. Your job in this problem is contribute a piece of the solution.

    The game is played with the computer and a deck of cards. Each card has on it one of four values (X, Y, Z, and N). Each player in turn gets five attempts to accumulate points. We call each attempt a round. After player A finishes his five rounds, it is player B's turn. Play continues until one of the players accumulates 100 points. Your job today is to ONLY design a finite state machine to keep track of the STATE of the current round. Each round starts in the intial state, where X=0 and Y=0. Cards from the deck are turned over one by one. Each card transitions the round from its current state to its next state, until the round terminates, at which point we'll start a new round in the initial state.

    The transistions are as follows:

    X: The number of X's is incremented, producing a new state for the round.

    Y: The number of Y's is incremented, producing a new state for the round.

    Z: If the number of X's is less than 2, the number of X's is incremented, producing a new state for the round. If the number of X's is 2, the state of the current round does not change.

    N: Other information on the card gives the number of points accumulated. N also terminates the current round.

    Important rule: If the number of X's or Y's reaches a count of 3, the current round is terminated and another round is started. When a round starts, its state is X=0, Y=0.

    Hint: Since the number of X's and Y's specify the state of the current round, how many possible states are needed to describe the state of the current round.

    Hint: A state can not have X=3, because then the round would be finished, and we would have started a *new* current round.

    On the diagram below, label each state. For each state draw an arrow showing the transition to the next state that would occur for each of the four inputs. (We have provided sixteen states. You will not need all of them. Use only as many as you need).

    Note, we did not specify outputs for these states. Therefore, your state machine will not include outputs. It will only include states and transistions represented by inputs.
  3. Trying Out Flip-Flops
    The Master-Slave flipflop we introduced in class is shown below.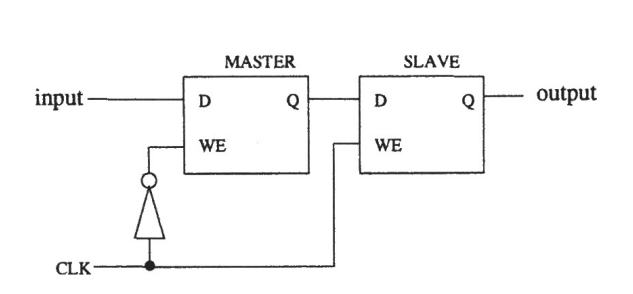
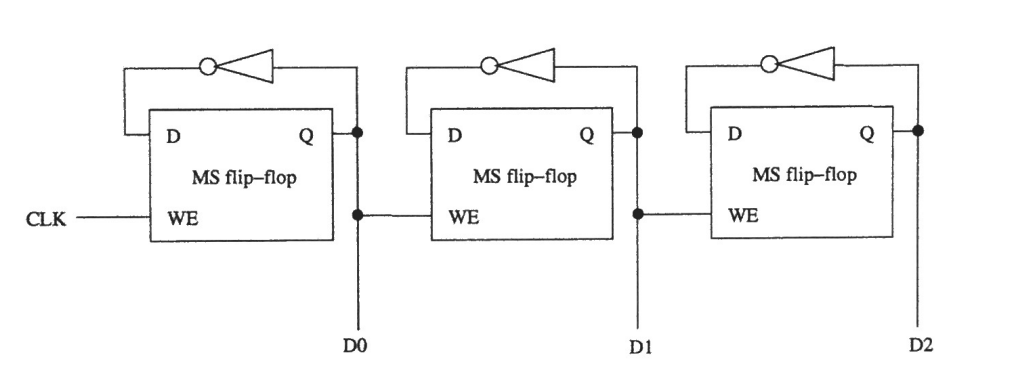
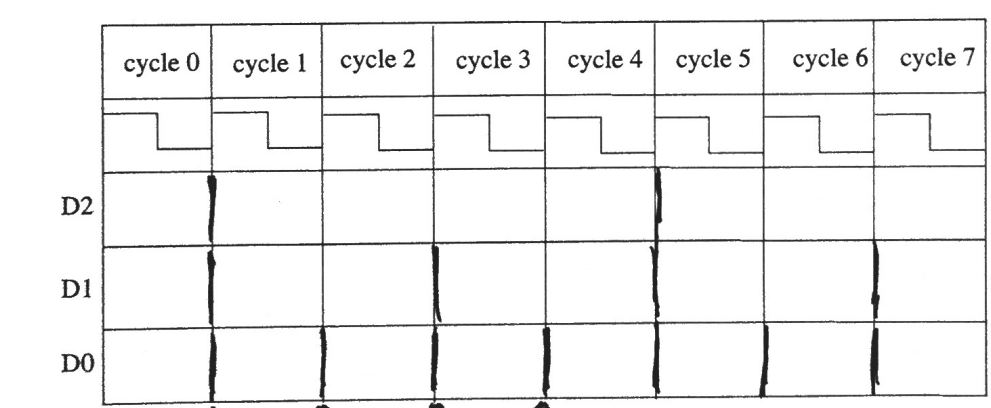
    Note that the input value is visible at the output after the clock transitions from 0 to 1. Shown below is a circuit constructed with three of these flipflops.
    Your job: Fill in the entries for D2, D1, D0 for each of clock cycles shown: (Addendum 10/12/17) In Cycle 0, all three flip-flops hold the value 0
    In 10 words or less, what is this circuit doing?
  1. Added (Updated for Clarity 10/12/17)
    Write a program in LC-3 machine language that places a 1 into R0 if the value in R1 is identical to the value in R2, and places a 0 into R0 if the values in R1 and R2 are different.

  2. Added
    What does the following program do (in 20 words or fewer):

    0101 100 100 1 00000
    1001 000 001 111111
    0001 000 000 1 00001
    0001 000 000 000 010
    0000 100 000000001
    0001 100 100 1 00001
    1111 0000 0010 0101

  3. Added
    What does the following program do (in 20 words or fewer):

    0101 000 000 1 00000
    0101 101 001 1 00001
    0000 101 000000001
    0001 000 000 1 00001
    1111 0000 0010 0101