Chapter 9: Structures

What's in Chapter 9?

Structure Declarations
Accessing elements of a structure
Initialization of structure data
Using pointers to access structures
Passing structures as parameters to functions
Example of a Linear Linked List
Example of a Huffman Code

A structure is a collection of variables that share a single name. In an array, each element has the same format. With structures we specify the types and names of each of the elements or members of the structure. The individual members of a structure are referenced by their subname. Therefore, to access data stored in a structure, we must give both the name of the collection and the name of the element. Structures are one of the most powerful features of the C language. In the same way that functions allow us to extend the C language to include new operations, structures provide a mechanism for extending the data types. With structures we can add new data types derived from an aggregate of existing types.

Structure Declarations

Like other elements of C programming, the structure must be declared before it can be used. The declaration specifies the tagname of the structure and the names and types of the individual members. The following example has three members: one 8-bit integer and two word pointers

struct theport{
   unsigned char mask;    // defines which bits are active
   unsigned long volatile *addr;  // pointer to its address
   unsigned long volatile *ddr;}; // pointer to its direction reg

The above declaration does not create any variables or allocate any space. Therefore to use a structure we must define a global or local variable of this type. The tagname (theport) along with the keyword struct can be used to define variables of this new data type:

struct theport PortA,PortB,PortE;

The above line defines the three variables and allocates 9 bytes for each of variable. Because the pointers will be 32-bit aligned the compiler will skip three bytes between mask and addr, so each object will occupy 12 bytes. If you knew you needed just three copies of structures of this type, you could have defined them as

struct theport{
   unsigned char mask;    // defines which bits are active
   unsigned long volatile *addr;
   unsigned long volatile *ddr;}PortA,PortB,PortE;

Definitions like the above are hard to extend, so to improve code reuse we can use typedef to actually create a new data type (called port in the example below) that behaves syntactically like char int short etc.

struct theport{
   unsigned char mask;    // defines which bits are active
   unsigned long volatile *addr;  // address
   unsigned long volatile *ddr;}; // direction reg
typedef struct theport port_t;
port_t PortA,PortB,PortE;

Once we have used typedef to create port_t, we don't need access to the name theport anymore. Consequently, some programmers use to following short-cut:

typedef struct {
   unsigned char mask;    // defines which bits are active
   unsigned long volatile *addr;        // address
   unsigned long volatile *ddr;}port_t; // direction reg
port_t PortA,PortB,PortE;

Similarly, I have also seen the following approach to creating structures that uses the same structure name as the typedef name:

struct port{
   unsigned char mask;    // defines which bits are active
   unsigned long volatile *addr;  // address
   unsigned long volatile *ddr;}; // direction reg
typedef struct port port;
port PortA,PortB,PortE;

Most compilers support all of the above methods of declaring and defining structures.

 

Accessing Members of a Structure

We need to specify both the structure name (name of the variable) and the member name when accessing information stored in a structure. The following examples show accesses to individual members:

PortB.mask = 0xFF;     // the TM4C123 has 8 bits on PORTB
PortB.addr = (unsigned long volatile *)(0x400053FC);
PortB.ddr = (unsigned long volatile *)(0x40005400);
PortE.mask = 0x3F;      // the TM4C123 has 6 bits on PORTE
PortE.addr = (unsigned long volatile *)(0x400243FC);
PortE.ddr = (unsigned long volatile *)(0x40024400);
(*PortE.ddr) = 0;               // specify PortE as inputs
(*PortB.addr) = (*PortE.addr);  // copy from PortE to PortB

The syntax can get a little complicated when a member of a structure is another structure as illustrated in the next example:

struct theline{
   int x1,y1;    // starting point
   int x2,y2;    // starting point
   unsigned char color;}; // color
typedef struct theline line_t;
struct thepath{
   line_t L1,L2;  // two lines
   char direction;};
typedef struct thepath path_t;
path_t p;        // global
void Setp(void){ line_t myLine; path_t q;
   p.L1.x1 = 5;  // black line from 5,6 to 10,12
   p.L1.y1 = 6;
   p.L1.x2 = 10;
   p.L1.y2 = 12;
   p.L1.color = 255;
   p.L2.x1 = 0;  // white line from 0,1 to 2,3
   p.L2.y1 = 1;
   p.L2.x2 = 2;
   p.L2.y2 = 3;
   p.L2.color = 0;
   p.direction = -1;
   myLine = p.L1;
   q = p;
};
Listing 9-1: Examples of accessing structures

 

The local variable declaration line myLine; will allocate 9 bytes on the stack while path q; will allocate 19 bytes on the stack. In actuality most C compilers in an attempt to maintain addresses as 32-bit aligned numbers will actually allocate 12 and 28 bytes respectively. In particular, the Cortex M executes faster if  accesses occur on word-aligned addresses. For example, a 32-bit data access to an odd address requires two bus cycles, while a 32-bit data access to a word-aligned address requires only one bus cycle.  Notice that the expression p.L1.x1 is of the type int, the term p.L1 has the type line, while just p has the type path. The expression q=p; will copy the entire 15 bytes that constitute the structure from p to q.

 

Initialization of a Structure

Just like any variable, we can specify the initial value of a structure at the time of its definition.

path_t thePath={{0,0,5,6,128},{5,6,-10,6,128},1}; 
line_t theLine={0,0,5,6,128}; 
port_t PortE={0x3F,
   (unsigned long volatile *)(0x400243FC),
   (unsigned long volatile *)(0x40024400)};

If we leave part of the initialization blank it is filled with zeros.

path_t thePath={{0,0,5,6,128},}; 
line_t thePath={5,6,10,12,}; 
port_t PortE={1,  (unsigned char volatile *)(0x100A),};

 

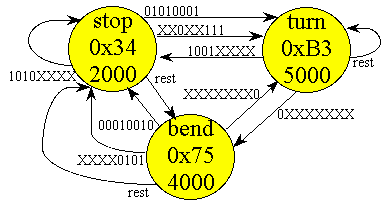
To place a structure in ROM, we define it as a global constant. In the following example the structure fsm[3] will be allocated and initialized in ROM-space. The linked-structure finite syatem machine is a good example of a ROM-based structure. For more information about finite state machines see either Section 6.5 of Embedded Systems: Introduction to ARM Cortex M Microcontrollers by Jonathan W. Valvano, or Section 3.5 of Embedded Systems: Real-Time Interfacing to ARM Cortex M Microcontrollers by Jonathan W. Valvano.

struct State{
    unsigned char Out;     /* Output to Port B */
    unsigned short Wait;   /* Time (62.5ns cycles) to wait */
    unsigned char AndMask[4];
    unsigned char EquMask[4];
    const struct State *Next[4];};  /* Next states */
typedef const struct State state_t;
typedef state_t * StatePtr;
#define stop &fsm[0]
#define turn &fsm[1]
#define bend &fsm[2]
state_t fsm[3]={
{0x34, 16000,   // stop 1 ms
   {0xFF,   0xF0,   0x27,   0x00},
   {0x51,   0xA0,   0x07,   0x00},
   {turn,   stop,   turn,   bend}},
{0xB3,40000,   // turn 2.5 ms
   {0x80,   0xF0,   0x00,   0x00},
   {0x00,   0x90,   0x00,   0x00},
   {bend,   stop,   turn,   turn}},
{0x75,32000,   // bend 2 ms
   {0xFF,   0x0F,   0x01,   0x00},
   {0x12,   0x05,   0x00,   0x00},
   {stop,   stop,   turn,   stop}}};
Listing 9-2: Example of initializing a structure in ROM

 

Using pointers to access structures

Just like other variables we can use pointers to access information stored in a structure. The syntax is illustrated in the following examples:


void Setp(void){ path_t *ppt;
   ppt = &p;        // pointer to an existing global variable
   ppt->L1.x1 = 5;  // black line from 5,6 to 10,12
   ppt->L1.y1 = 6;
   ppt->L1.x2 = 10;
   ppt->L1.y2 = 12;
   ppt->L1.color = 255;
   ppt->L2.x1 = 0;  // white line from 0,1 to 2,3
   ppt->L2.y1 = 1;
   ppt->L2.x2 = 2;
   ppt->L2.y2 = 3;
   ppt->L2.color = 0;
   ppt->direction = -1;
   (*ppt).direction = -1;
};
Listing 9-3: Examples of accessing a structure using a pointer

Notice that the syntax ppt->direction is equivalent to (*ppt).direction. The parentheses in this access are required, because along with () and [], the operators . and -> have the highest precedence and associate from left to right. Therefore *ppt.direction would be a syntax error because ppt.direction can not be evaluated.

As an another example of pointer access consider the finite state machine controller for the fsm[3] structure shown above. The state machine is illustrated in Figure 9-1, and the program shown in Listing 9-4. There is an example in Chapter 10 that extends this machine to implement function pointers.

Figure 9-1: State machine

 

void control(void){ StatePtr Pt;
 unsigned char Input; unsigned int i;
  SysTick_Init();
  Port_Init();
  Pt = stop;       // Initial State 
  while(1){
    GPIO_PORTA_DATA_R = Pt->Out; // 1) output
    SysTick_Wait(Pt->Wait);      // 2) wait 
    Input = GPIO_PORTB_DATA_R;   // 3) input 
    for(i=0;i<4;i++)
      if((Input&Pt->AndMask[i])==Pt->EquMask[i]){
        Pt = Pt->Next[i]; // 4) next depends on input
        i=4; }}};
Listing 9-4: Finite state machine controller for TM4C123

 

Passing Structures to Functions

Like any other data type, we can pass structures as parameters to functions. Because most structures occupy a large number of bytes, it makes more sense to pass the structure by reference rather than by value. In the following "call by value" example, the entire 12-byte structure is copied on the stack when the function is called.

unsigned long Input(port_t thePort){
   return (*thePort.addr);}

When we use "call by reference", a pointer to the structure is passed when the function is called.

typedef const struct {
  unsigned char mask;    // defines which bits are active
  unsigned long volatile *addr;      // address
  unsigned long volatile *ddr;}port; // direction reg
port_t PortE={0x3F,
   (unsigned long volatile *)(0x400243FC),
   (unsigned long volatile *)(0x40024400)};
port_t PortF={0x1F,  
  (unsigned long volatile *)(0x400253FC),
  (unsigned long volatile *)(0x40025400)};
int MakeOutput(port_t *ppt){
  (*ppt->ddr) = ppt->mask; // make output
  return 1;}
int MakeInput(port_t *ppt){
  (*ppt->ddr )= 0x00; // make input
  return 1;}
unsigned char Input( port_t *ppt){
 return (*ppt->addr);}
void Output(port_t *ppt, unsigned char data){
 (*ppt->addr) = data;
}
int main(void){ unsigned char MyData;
  MakeInput(&PortE);
  MakeOutput(&PortF);
  Output(&PortF,0);
  MyData=Input(&PortE);
  return 1;}
Listing 9-5: Port access organized with a data structure

 


Linear Linked Lists

One of the applications of structures involves linking elements together with pointers. A linear linked list is a simple 1-D data structure where the nodes are chained together one after another. Each node contains data and a link to the next node. The first node is pointed to by the HeadPt and the last node has a null-pointer in the next field. A node could be defined as

struct node{
  unsigned short data;  // 16 bit information
  struct node *next;    // pointer to the next
};
typedef struct node node_t;
node_t *HeadPt;
Listing 9-8: Linear linked list node structure

 

Figure 9-3: Linear linked list with 3 nodes

In order to store more data in the structure, we will first create a new node then link it into the list. The routine StoreData will return a true value if successful.

#include <stdlib.h>;
int StoreData(unsigned short info){ node_t *pt;
  pt=malloc(sizeof(node_t));  // create a new entry
  if(pt){
    pt->data=info;              // store data
    pt->next=HeadPt;            // link into existing
    HeadPt=pt;
    return(1);
  }
  return(0);      // out of memory
};
Listing 9-9: Code to add a node at the beginning of a linear linked list

In order to search the list we start at the HeadPt, and stop when the pointer becomes null. The routine Search will return a pointer to the node if found, and it will return a null-pointer if the data is not found.

node_t *Search(unsigned short info){node_t *pt;
  pt=HeadPt;
  while(pt){
    if(pt->data==info)
        return (pt);
    pt=pt->next;   // link to next
  }
  return(pt);      // not found
};
Listing 9-10: Code to find a node in a linear linked list

To count the number of elements, we again start at the HeadPt, and stop when the pointer becomes null. The routine Count will return the number of elements in the list.

unsigned short Count(void){ node_t *pt;
  unsigned short cnt;
  cnt = 0;
  pt = HeadPt;
  while(pt){
    cnt++;
    pt = pt->next;   // link to next
  }
  return(cnt);
};
Listing 9-11: Code to count the number of nodes in a linear linked list

If we wanted to maintain a sorted list, then we can insert new data at the proper place, in between data elements smaller and larger than the one we are inserting. In the following figure we are inserting the element 250 in between elements 200 and 300.

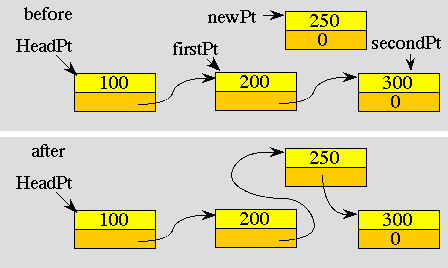
Figure 9-4: Inserting a node in sorted order

In case 1, the list is initially empty, and this new element is the first and only one. In case 2, the new element is inserted at the front of the list because it has the smallest data value. Case 3 is the general case depicted in the above figure. In this situation, the new element is placed in between firstPt and secondPt. In case 4, the new element is placed at the end of the list because it has the largest data value.

int InsertData(unsigned short info){
node_t *firstPt,*secondPt,*newPt;
  newPt = malloc(sizeof(node_t));  // create a new entry
  if(newPt){
    newPt->data = info;              // store data
    if(HeadPt==0){   // case 1
      newPt->next = HeadPt;   // only element
      HeadPt = newPt;
      return(1);
    }
    if(info<=HeadPt->data){ // case 2
      newPt->next = HeadPt;   // first element in list
      HeadPt = newPt;
      return(1);
    }
    firstPt = HeadPt;   // search from beginning
    secondPt = HeadPt->next; 
    while(secondPt){
      if(info <= secondPt->data){ // case 3
        newPt->next = secondPt;   // insert element here
        firstPt->next = newPt;
        return(1);
      }
      firstPt = secondPt;   // search next
      secondPt = secondPt->next; 
    }
    newPt->next = secondPt;   // case 4, insert at end
    firstPt->next = newPt;
    return(1);
  }
  return(0);      // out of memory
};
Listing 9-12: Code to insert a node in a sorted linear linked list

The following function will search and remove a node from the linked list. Case 1 is the situation in which an attempt is made to remove an element from an empty list. The return value of zero signifies the attempt failed. In case 2, the first element is removed. In this situation the HeadPt must be updated to now point to the second element. It is possible the second element does not exist, because the list orginally had only one element. This is OK because in this situation HeadPt will be set to null signifying the list is now empty. Case 3 is the general situation in which the element at secondPt is removed. The element before, firstPt, is now linked to the element after. Case 4 is the situation where the element that was requested to be removed did not exist. In this case, the return value of zero signifies the request failed.

int Remove(unsigned short info){
node_t *firstPt,*secondPt;
  if(HeadPt==0)  // case 1
    return(0);   // empty list
  firstPt = HeadPt;
  secondPt = HeadPt->next;
  if(info==HeadPt->data){  // case 2
    HeadPt = secondPt; // remove first element in list
    free(firstPt);     // return unneeded memory to heap
    return(1);
  }
  while(secondPt){
    if(secondPt->data==info){  // case 3
      firstPt->next=secondPt->next; // remove this one
      free(secondPt);   // return unneeded memory to heap
      return(1);
    }
    firstPt = secondPt;   // search next
    secondPt = secondPt->next; 
  }
  return(0);    // case 4, not found
};
Listing 9-13: Code to remove a node from a sorted linear linked list

Example of a Huffman Code

When information is stored or transmitted there is a fixed cost for each bit. Data compression and decompression provide a means to reduce this cost without loss of information. If the sending computer compresses a message before transmission and the receiving computer decompresses it at the destination, the effective bandwidth is increased. In particular, this example introduces a way to process bit streams using Huffman encoding and decoding. A typical application is illustrated by the following flow diagram.

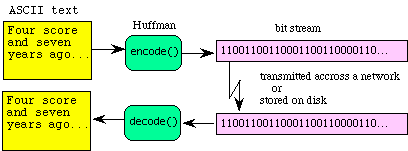
Figure 9-5: Data flow diagram showing a typical application of Huffman encoding and decoding

 

The Huffman code is similar to the Morse code in that they both use short patterns for letters that occur more frequently. In regular ASCII, all characters are encoded with the same number of bits (8). Conversely, with the Huffman code, we assign codes where the number of bits to encode each letter varies. In this way, we can use short codes for letter like "e s i a t o n" (that have a higher probability of occurrence) and long codes for seldom used consonants like "j q w z" (that have a lower probability of occurrence). To illustrate the encode-decode operations, consider the following Huffman code for the letters M,I,P,S. S is encoded as "0", I as "10", P as "110" and M as "111". We can store a Huffman code as a binary tree.

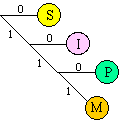
Figure 9-6: Huffman code for the letters S I P M

 

If "MISSISSIPPI" were to be stored in ASCII, it would require 10 bytes or 80 bits. With this simple Huffman code, the same string can be stored in 21 bits.

Figure 9-7: Huffman encoding for MISSISSIPPI

 

Of course, this Huffman code can only handle 4 letters, while the ASCII code has 128 possibilities, so it is not fair to claim we have an 80 to 21 bit savings. Nevertheless, for information that has a wide range of individual probabilities of occurrence, a Huffman code will be efficient. In the following implementation the functions BitPut() and BitGet() are called to save and recover binary data. The implementations of these two functions were presented back in Chapter 2.

 

struct Node{
    char Letter0;     // ASCII code if binary 0
    char Letter1;     // ASCII code if binary 1
// Letter1 is NULL(0) if Link is pointer to another node
    const struct Node *Link;};  // binary tree pointer 
typedef const struct Node node_t;
// Huffman tree
node_t twentysixth= {'Q','Z',0};
node_t twentyfifth= {'X',0,&twentysixth}; 
node_t twentyfourth={'G',0,&twentyfifth}; 
node_t twentythird= {'J',0,&twentyfourth}; 
node_t twentysecond={'W',0,&twentythird}; 
node_t twentyfirst= {'V',0,&twentysecond}; 
node_t twentyth=    {'H',0,&twentyfirst}; 
node_t ninteenth=   {'F',0,&twentyth}; 
node_t eighteenth=  {'B',0,&ninteenth}; 
node_t seventeenth= {'K',0,&eighteenth}; 
node_t sixteenth=   {'D',0,&seventeenth}; 
node_t fifteenth=   {'P',0,&sixteenth}; 
node_t fourteenth=  {'M',0,&fifteenth}; 
node_t thirteenth=  {'Y',0,&fourteenth}; 
node_t twelfth=     {'L',0,&thirteenth}; 
node_t eleventh=    {'U',0,&twelfth}; 
node_t tenth=       {'R',0,&eleventh}; 
node_t ninth=       {'C',0,&tenth}; 
node_t eighth=      {'O',0,&ninth}; 
node_t seventh=     {' ',0,&eighth}; 
node_t sixth=       {'N',0,&seventh}; 
node_t fifth=       {'I',0,&sixth}; 
node_t fourth=      {'S',0,&fifth}; 
node_t third=       {'T',0,&fourth}; 
node_t second=      {'A',0,&third}; 
node_t root=        {'E',0,&second};
//********encode*************** 
// convert ASCII string to Huffman bit sequence
// returns bit count if OK
// returns 0         if BitFifo Full
// returns 0xFFFF    if illegal character
int encode(char *sPt){  // null-terminated ASCII string
 int NotFound; char data;
 int BitCount=0;       // number of bits created
 node_t *hpt;          // pointer into Huffman tree
 while (data=(*sPt)){
   sPt++;              // next character
   hpt=&root;          // start search at root
   NotFound=1;         // changes to 0 when found
   while(NotFound){
     if ((hpt->Letter0)==data){
       if(!BitPut(0)) 
         return (0);   // data structure full
       BitCount++;
       NotFound=0; }
     else {
       if(!BitPut(1)) 
         return (0);   // data structure full
       BitCount++;
      if ((hpt->Letter1)==data)        
         NotFound=0;
       else {      // doesn't match either Letter0 or Letter1
         hpt=hpt->Link;
         if (hpt==0) return (0xFFFF); // illegal, end of tree?
       }
     }
   }
  }
  return BitCount;        
 }
//********decode*************** 
// convert Huffman bit sequence to ASCII
// will remove from the BitFifo until it is empty
// returns character count
int decode(char *sPt){  // null-terminated ASCII string
 int CharCount=0;       // number of ASCII characters created
 unsigned int data;
 node_t *hpt;           // pointer into Huffman tree
 hpt=&root;             // start search at root
 while (BitGet(&data)){     
   if (data==0){
     (*sPt)= (hpt->Letter0);
     sPt++;
     CharCount++;
     hpt=&root;}      // start over and search at root
   else  //data is 1
     if((hpt->Link)==0){ 
       (*sPt)= (hpt->Letter1);
       sPt++;
       CharCount++;
       hpt=&root;}    // start over and search at root
     else {       // doesn't match either Letter0 or Letter1
       hpt=hpt->Link;
     }
   }
   (*sPt)=0;  // null terminated
   return CharCount;        
 }
Listing 9-14: A Huffman code implementation

 

 

Go to Chapter 10 on Functions Return to Table of Contents