Seismic Wave Migration
Lecture by Prof. Brian L. Evans (UT Austin)
Based on Lecture Notes by Prof. Russell M. Mersereau (Georgia Tech)
Scribe: Mr. Er-Hsien Fu
THE SEISMIC PROBLEM
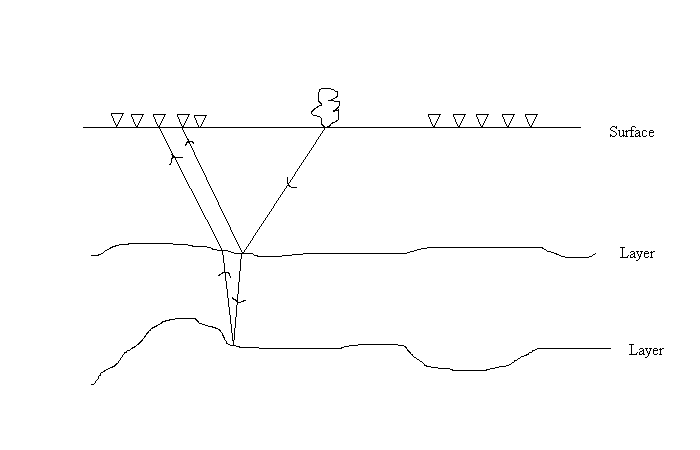
- Source is nearly impulsive
- Received signal contains multiple reflections
- Arrival times of reflected signals are of interest
- Data is "stacked" so that the received signal is "as if" source and receiver are at the same point
THE MIGRATION PROBLEM
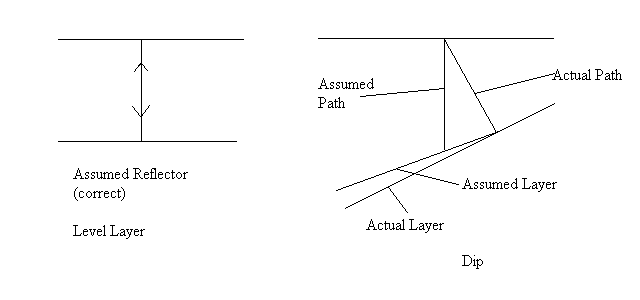
- We can compensate for this effect if the acoustic velocity is known
- Determining the acoustic velocity is itself a difficult problem
THE APPROACH
Measurements made at surface
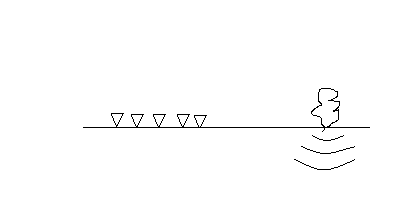
- A reflection from a point sets off an expanding spherical wavefront
- This propagates according to the acoustic wave equation
- The actual recorded signal is complicated
- Propagation governed by the 2-D hyperbolic wave equation
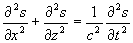
- The wave field becomes less complicated and easier to interpret, if we could look at it at a greater depth. This is equivalent to looking at it in an earlier time
- s(x,0,t) can be measured at the surface—serves as a boundary condition for the partial differential equation
- We want s(x,zo,t), which is the wave profile at depth zo
- Approach is to use the wave equation to propagate s(x,z,t) backwards from depth z from 0 to zo, which is called migration. We want to extrapolate from s(x, z0, t) to s(x, z0 + Dz, t).
DEVELOPMENT
Define the 2-D Fourier transform of the wave field with respect to x and t at depth z
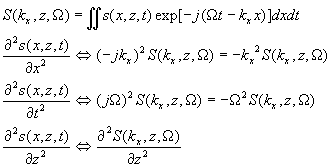
- Taking the Fourier transform of both sides of the wave equation
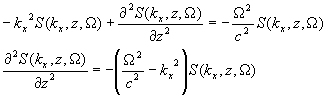
We have turned a partial differential equation in the space-time domain into an ordinary differential equation in the wavenumber-frequency domain.
CONTINUOUS SOLUTION
Case 1:
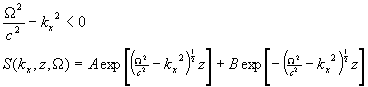

- These solutions do not correspond to propagating waves
- They can be eliminated on physical grounds
Case 2:
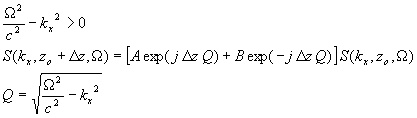
- The positive exponent corresponds to an upwardly propagating wave.
- The negative exponent corresponds to a downwardly propagating wave. Set B=0.
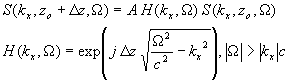
- The necessary extrapolation can be performed using a linear, shift-invariant filter
- The desired frequency response is all-pass with a hyperbolic phase response.
DISCRETIZED SOLUTION
For sampled measurements s(n1D
x, lD
z, n2D
t), the extrapolation can be performed by a digital filter. Let
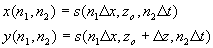
 )
)
where w
1 = wavenumber kx and w
2 = temporal frequency W
and
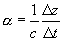
- For |a
w
2| > |w
1|, transfer function has unit magnitude and phase
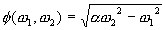
and corresponds to propagating waves.
- In the evanescent region, |a
w
2| < |w
1|, waves do not propagate but are attenuated.
Filter design problem. We design either
- an all-pass filter with the proper phase characteristic
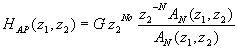
- a fan filter where the Propagating Region is the passband and the Evanescent Region is the stopband (pages 274-275 of the first edition of Dudgeon & Mersereau).
evanescent- tending to vanish or pass away like vapor



![]()
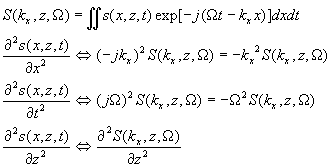
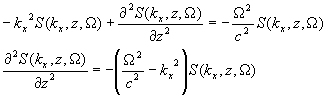
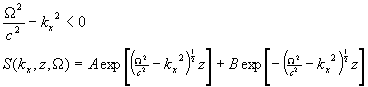
![]()
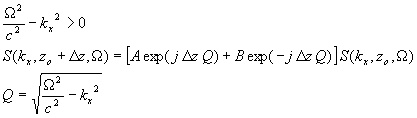
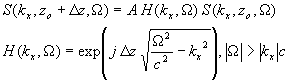
![]()
![]() )
)![]()
![]()
![]()