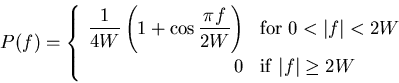EE445S Real-Time Digital Signal Processing Laboratory
Handout G: Raised Cosine Pulse
Section 7.5, pp. 431-434,
Simon Haykin, Communication Systems, 4th ed.
We may overcome the practical difficulties encounted with the ideal Nyquist
channel by extending the bandwidth from the minimum value 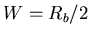 to
an adjustable value between
to
an adjustable value between 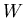 and
and 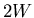 .
We now specify the frequency function
.
We now specify the frequency function 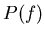 to satisfy a condition
more elaborate than that for the ideal Nyquist channel; specifically,
we retain three terms of (7.53) and restrict the frequency band of
interest to
to satisfy a condition
more elaborate than that for the ideal Nyquist channel; specifically,
we retain three terms of (7.53) and restrict the frequency band of
interest to ![$[-W, W]$](img5.gif) , as shown by
, as shown by
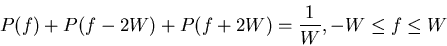 |
(1) |
We may devise several band-limited functions to satisfy
(1).
A particular form of 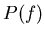 that embodies many desirable features
is provided by a raised cosine spectrum.
This frequency characteristic consists of a flat portion and a rolloff
portion that has a sinusoidal form, as follows:
that embodies many desirable features
is provided by a raised cosine spectrum.
This frequency characteristic consists of a flat portion and a rolloff
portion that has a sinusoidal form, as follows:
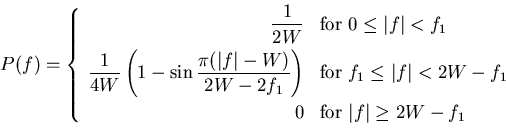 |
(2) |
The frequency parameter 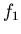 and bandwidth
and bandwidth 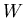 are related by
are related by
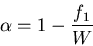 |
(3) |
The parameter 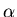 is called the rolloff factor; it indicates the
excess bandwidth over the ideal solution,
is called the rolloff factor; it indicates the
excess bandwidth over the ideal solution, 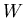 .
Specifically, the transmission bandwidth
.
Specifically, the transmission bandwidth 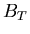 is defined by
is defined by
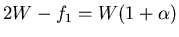 .
.
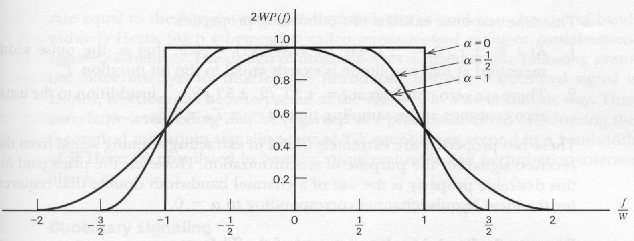
The frequency response  , normalized by multiplying it by
, normalized by multiplying it by 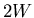 ,
is shown plotted in Fig. 1 for three values
of
,
is shown plotted in Fig. 1 for three values
of 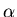 , namely, 0, 0.5, and 1.
We see that for
, namely, 0, 0.5, and 1.
We see that for 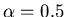 or 1, the function
or 1, the function 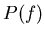 cuts off
gradually as compared with the ideal Nyquist channel (i.e.,
cuts off
gradually as compared with the ideal Nyquist channel (i.e., 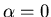 )
and is therefore easier to implement in practice.
Also the function
)
and is therefore easier to implement in practice.
Also the function 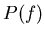 exhibits odd symmetry with respect to the
Nyquist bandwidth
exhibits odd symmetry with respect to the
Nyquist bandwidth 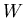 , making it possible to satisfy the condition of
(1).
The time response
, making it possible to satisfy the condition of
(1).
The time response 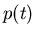 is the inverse Fourier transform of the
function
is the inverse Fourier transform of the
function 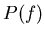 .
Hence, using the
.
Hence, using the 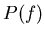 defined in (2),
we obtain the result (see Problem 7.9)
defined in (2),
we obtain the result (see Problem 7.9)
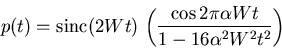 |
(4) |
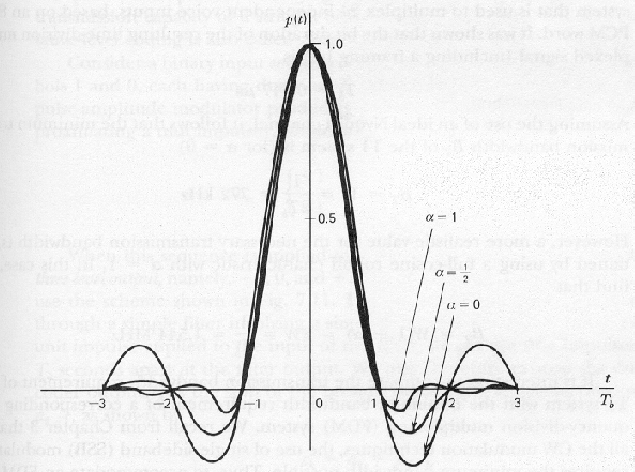
which is shown plotted in Fig. 2 for
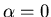 , 0.5, and 1.
The function
, 0.5, and 1.
The function 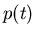 consists of the product of two factors:
the factor
consists of the product of two factors:
the factor
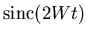 characterizing the ideal Nyquist channel
and a second factor that decreases as
characterizing the ideal Nyquist channel
and a second factor that decreases as 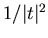 for large
for large 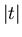 .
The first factor ensures zero crossings of
.
The first factor ensures zero crossings of 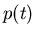 at the desired
sampling instants of time
at the desired
sampling instants of time 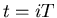 with
with 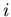 an integer (positive
and negative).
The second factor reduces the tails of the pulse considerably below
that obtained from the ideal Nyquist channel, so that the transmission
of binary waves using such pulses is relatively insensitive to sampling
time errors.
In fact, for
an integer (positive
and negative).
The second factor reduces the tails of the pulse considerably below
that obtained from the ideal Nyquist channel, so that the transmission
of binary waves using such pulses is relatively insensitive to sampling
time errors.
In fact, for 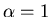 , we have the most gradual rolloff in that
the amplitudes of the oscillatory tails of
, we have the most gradual rolloff in that
the amplitudes of the oscillatory tails of 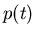 are smallest.
Thus, the amount of intersymbol interference resulting from timing
error decreases as the rolloff factor
are smallest.
Thus, the amount of intersymbol interference resulting from timing
error decreases as the rolloff factor 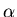 is increased from zero to unity.
is increased from zero to unity.
Figure 1:
Frequency response for the raised cosine function.
 |
The special case with 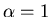 (i.e.,
(i.e.,  ) is known as the
full-cosine rolloff characteristic, for which the frequency
response of (2) simplifies to
) is known as the
full-cosine rolloff characteristic, for which the frequency
response of (2) simplifies to
Correspondingly, the time response 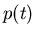 simplifies to
simplifies to
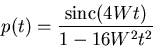 |
(5) |
The time response exhibits two interesting properties:
- At
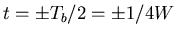 , we have
, we have 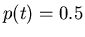 ; that is,
the pulse width measured at half amplitude is exactly equal
to the bit duration
; that is,
the pulse width measured at half amplitude is exactly equal
to the bit duration 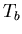 .
.
- There are zero crossings at
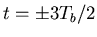 ,
, 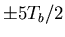 ,...
in addition to the usual zero crossings at the sampling times
,...
in addition to the usual zero crossings at the sampling times
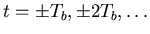
These two properties are extremely useful in extracting a timing signal from
the received signal for the purpose of synchronization.
However, the price paid for this desirable property is the use of a
channel bandwidth double that required for the ideal Nyquist channel
corresponding to 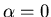 .
.
Figure 2:
Time response for the raised cosine function.
 |
Placeholder - please ignore.
Brian L. Evans
![]() to
an adjustable value between
to
an adjustable value between ![]() and
and ![]() .
We now specify the frequency function
.
We now specify the frequency function ![]() to satisfy a condition
more elaborate than that for the ideal Nyquist channel; specifically,
we retain three terms of (7.53) and restrict the frequency band of
interest to
to satisfy a condition
more elaborate than that for the ideal Nyquist channel; specifically,
we retain three terms of (7.53) and restrict the frequency band of
interest to ![]() , as shown by
, as shown by
![]() , normalized by multiplying it by
, normalized by multiplying it by ![]() ,
is shown plotted in Fig. 1 for three values
of
,
is shown plotted in Fig. 1 for three values
of ![]() , namely, 0, 0.5, and 1.
We see that for
, namely, 0, 0.5, and 1.
We see that for ![]() or 1, the function
or 1, the function ![]() cuts off
gradually as compared with the ideal Nyquist channel (i.e.,
cuts off
gradually as compared with the ideal Nyquist channel (i.e., ![]() )
and is therefore easier to implement in practice.
Also the function
)
and is therefore easier to implement in practice.
Also the function ![]() exhibits odd symmetry with respect to the
Nyquist bandwidth
exhibits odd symmetry with respect to the
Nyquist bandwidth ![]() , making it possible to satisfy the condition of
(1).
The time response
, making it possible to satisfy the condition of
(1).
The time response ![]() is the inverse Fourier transform of the
function
is the inverse Fourier transform of the
function ![]() .
Hence, using the
.
Hence, using the ![]() defined in (2),
we obtain the result (see Problem 7.9)
defined in (2),
we obtain the result (see Problem 7.9)
![]() (i.e.,
(i.e., ![]() ) is known as the
full-cosine rolloff characteristic, for which the frequency
response of (2) simplifies to
) is known as the
full-cosine rolloff characteristic, for which the frequency
response of (2) simplifies to