- "But what is the Fourier Transform? A visual introduction", by 3Blue1Brown, Jan. 26, 2018
 Videos:
Brian Douglas (13:03) -
Darryl Morrell, Part 1 (9:02) -
Darryl Morrell, Part 2 (11:07)
Videos:
Brian Douglas (13:03) -
Darryl Morrell, Part 1 (9:02) -
Darryl Morrell, Part 2 (11:07)
- Lecture Slides: Frequency Response - Fourier Transforms - Sampling & Reconstruction
- Handout Q Intro to Fourier Transforms
- Pictorial guide of Fourier transform pairs in Hz and rad/s in Appendix D of Michael Roberts' Fundamentals of Signals & Systems (course Canvas site only). Continuous-time Fourier transforms in terms of w in rad/s will have the same shape as those in terms of Hz; the ony difference is a scaling of the frequency axis by w = 2 pi f.
Approach #1. We are treating the signal as the impulse response of an LTI system.
In order to have a frequency response that is bounded in magnitude over all frequenices, the LTI system must be bounded-input bounded-output (BIBO) stable.
In continuous time, a BIBO stable LTI system must have its transfer function in the Laplace domain have a region of convergence that includes the imaginary axis s = j w. For a causal system, this means that the poles must be in the left-half of the Laplace plane. (The equivalent condition for a causal discrete-time LTI system is that all poles must be included the unit circle.)
For this second part, the impulse responses in parts (a) and (c) represent BIBO unstable systems because the region of convergence does not include the imaginay (j w) axis, and hence the frequency selectivity cannot be determined. And that would sufficient for an answer in those two cases.
Approach #2. On the other hand, we could analyze the frequency content of the signal. To determine the frequency content in each signal, one can either
- convert the Laplace transform to the frequency domain by substituting s = j w if the the substitution is valid, i.e. the region of convergence for the Laplace transform includes the imaginary axis, or
- compute the continuous-time Fourier transform of the signal
The Fourier transform of the unit step u(t) is
pi delta(w) + 1 / (j w)That transform pair is the second entry in the visual dictionary of Fourier transform pairs.
For part (a), we can compute the Fourier transform of cos(w0 t) u(t) using the Fourier transform property that multiplication in the time domain is convolution in the frequency domain:
X(j w) = (1/(2 pi)) F{ cos(w0 t) } * F{ u(t) }
X(j w) = (1/(2 pi)) (pi delta(w + w0) + pi delta(w - w0)) * ( pi delta(w) + 1 / (j w) )
Recall that
delta(w) * G(w) = G(w)
delta(w - w0) * G(w) = G(w - w0)
X(j w) = (1/2) ( pi delta(w + w0) + pi delta(w - w0) ) + 1 / ( j (w + w0) ) + 1 / ( j (w - w0) )
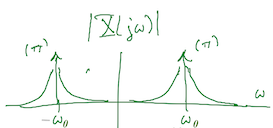
A plot of |X(j w)| is below:
Note that |X(j w)| is unbounded at w = w0 due to the 1 / ( j (w - w0) ) term and unbounded at w = -w0 due to the 1 / ( j (w + w0) ) term. The frequency content has a bandpass shape.
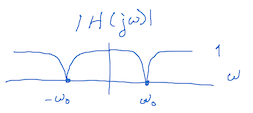
A notch filter eliminates a specific frequency w0. Recall that a cosine of frequency w0 also has a frequency component at -w0:
cos( w0 t ) = (1/2) e-j w0 t + (1/2) ej w0 t
The notch filter would remove frequencies at w0 and -w0.
Here's an example notch filter magnitude response:
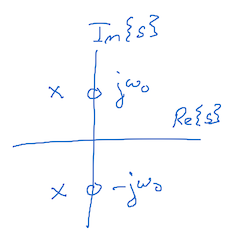
Here's an example pole-zero configuration in the Laplace domain for the above filter:
 bevans@ece.utexas.edu
bevans@ece.utexas.edu