1045
SigPy.RF: Comprehensive Open-Source RF Pulse Design Tools for Reproducible Research1Biomedical Engineering, Vanderbilt University, Nashville, TN, United States, 2Electrical Engineering, Stanford University, Stanford, CA, United States, 3Electrical Engineering and Computer Sciences, University of California, Berkeley, Berkeley, CA, United States, 4Electrical and Computer Engineering, UT Austin, Austin, TX, United States
Synopsis
We present SigPy.RF, an extensive set of open-source, Python-based tools for MRI RF pulse design. This toolbox extends the SigPy Python software package and leverages SigPy’s existing capabilities for GPU computation, iterative optimization, and powerful abstractions for linear operators, proximal operators, and applications. Tools are available for all steps of the excitation design process including trajectory/gradient design, pulse design, and simulation. Our implemented functions for pulse design include advanced SLR, multiband, adiabatic, optimal control, B$$$_1^+$$$-selective and small-tip pTx designers. SigPy.RF pulse designs were validated in simulations and a pTx experiment.
Target Audience
MRI RF pulse and sequence developers and educators.Introduction
While RF pulse developers increasingly share code online in independent repositories, no unified set of common pulse design tools is maintained in a rigorous and consistent manner with easy-to-read code and tutorials. An open source pulse design code library would facilitate the development and dissemination of novel techniques and the comparison of approaches, similar to how BART$$$^1$$$, SigPy$$$^2$$$, and MIRT$$$^3$$$ have made advanced parallel imaging and compressed sensing reconstruction methods widely accessible. To meet this need, we have developed a library of pulse design tools as part of the SigPy Python package$$$^2$$$, which we call SigPy.RF. Here we detail the software’s organization and goals, provide examples, and show an experimental validation of parallel transmission (pTx) pulses designed using SigPy.RF.Software Design
SigPy was chosen as a host software project because image reconstruction and RF pulse design require many of the same computational operations, and we can take advantage of SigPy’s powerful optimization tools, unified CPU and GPU interface, machine learning extensions, and sophisticated linear operator and application classes for pulse design, where they will be especially valuable for large non-linear and constrained parallel transmit (pTx) design problems. Python code is also easy-to-read and can be executed as a standalone program or using Jupyter notebooks, making it well-suited to both research and education. Figure 1 shows where the .rf tools fit into the SigPy function hierarchy, as a subclass of its .mri functions. Table 1 lists SigPy.RF’s currently implemented functions and planned pTx pulse design tools. These include tools for advanced SLR, multiband, adiabatic, optimal control, B$$$_1^+$$$-selective and small-tip pTx pulse design, along with functions for k-space/gradient trajectory design and Bloch simulation. Computationally intensive functions, such as Bloch simulators and the small-tip pTx designer include the option of GPU acceleration using SigPy’s CPU/GPU selection interface. SigPy.RF’s small-tip spatial domain parallel transmit pulse designer$$$^4$$$, rf.stspa(), includes options such as Tikhonov regularization, B$$$_0$$$ inhomogeneity correction, and instantaneous and average power constraints. Constrained optimization of pTx pulses is performed using the primal-dual hybrid gradient method$$$^5$$$ and SigPy’s proximal operator classes. Forthcoming pTx design functions listed in Table 1 include large-tip pTx design, as well designers for blipped trajectories such as $$$k_T$$$-points, spokes, echo-planar, and echo-planar shutter excitation pulses. A quadratically constrained quadratic program solver is also forthcoming, to enable local SAR-constrained pulse design for all pTx pulse types.Examples
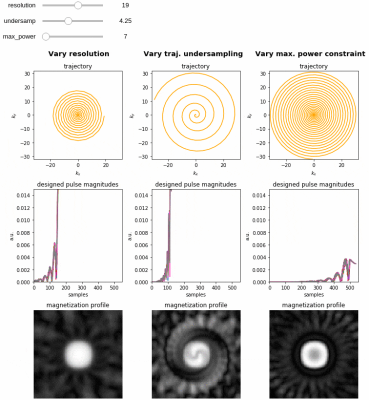
Figure 2 illustrates an interactive pTx small-tip spiral spatial domain pulse design performed with SigPy.RF’s stspa() function, in a Jupyter notebook. With only a few lines of code (see Figure 3), a spiral trajectory and the corresponding gradients are generated, the design is performed using stspa(), and the pulse is simulated to obtain the excited magnetization profile using a Linop object. Figure 4 shows predicted and imaged spiral excitation patterns in a phantom using 8 transmit channels on a 7T Philips Achieva scanner (Philips Healthcare, Best, Netherlands). maps were measured on the scanner, then exported and used in a SigPy pulse design, and the designed pulses were sent back to the scanner.Availability
The latest version of SigPy includes the most stable pulse design tools developed, and is available from https://github.com/mikgroup/sigpy and can be installed through conda or pip. The SigPy.RF fork including pulse design tools still under development can be downloaded from https://github.com/jonbmartin/sigpy-rf. Jupyter notebook pulse design tutorials for SigPy.RF can be downloaded from https://github.com/jonbmartin/sigpy-rf-tutorials. An educational workshop on SigPy.RF will be held at the 2020 ISMRM Annual Meeting and Exhibition.Discussion and Conclusion
We presented a comprehensive Python-based RF pulse design toolbox. Full end-to-end designs, including trajectory and gradient design, pulse design, and simulation can be completed with SigPy.RF, which will facilitate development of new pulse designs and pulse sequences, as well as RF pulse education. Currently the software includes designers for adiabatic, SLR, multiband, gSlider, B$$$_1^+$$$-selective, optimal control and small-tip pTx pulses, along with gradient trajectory and Bloch simulation tools. A major aim is to implement a comprehensive set of state-of-the-art pTx pulse design tools in the package, which will take advantage of SigPy’s proximal optimization, GPU, and linear operator functionality.Acknowledgements
The authors thank Zhipeng Cao of Vanderbilt University for his assistance with the pTx experiment. This work was supported by NIH grant R01 EB 016695.References
1. Uecker, M. et al. Berkeley Advanced Reconstruction Toolbox. Proc. ISMRM Annu. Meet. Exhib. (2015).
2. Ong, F., Lustig, M. SigPy: A Python Package for High Performance Iterative Reconstruction. Proc. ISMRM Annu. Meet. Exhib. (2019).
3. Fessler, J. A. Michigan Image Reconstruction Toolbox, available at https://web.eecs.umich.edu/~fessler/code/. Downloaded Nov 2019.
4. Grissom, W. et al. Spatial domain method for the design of RF pulses in multicoil parallel excitation. Magn. Reson. Med. 56, 620–629 (2006).
5. Chambolle, A. & Pock, T. A first-order primal-dual algorithm for convex problems with applications to imaging. (2010).
6. Staewen, R. S. et al. 3-D FLASH Imaging using a single surface coil and a new adiabatic pulse, BIR-4. Invest. Radiol. 25, 559–567 (1990).
7. Baum, J., Tycko, R. & Pines, A. Broadband and adiabatic inversion of a two-level system by phase-modulated pulses. Phys. Rev. A 32, 3435–3447 (1985).
8. Kupce, E. & Freeman, R. Stretched Adiabatic Pulses for Broadband Spin Inversion. J. Magn. Reson. Ser. A 117, 246–256 (1995).
9. Grissom, W. A., Cao, Z. & Does, M. D. |B1+|-selective excitation pulse design using the Shinnar–Le Roux algorithm. J. Magn. Reson. 242, 189–196 (2014).
10. Wong, E. Optimized Phase Schedules for Minimizing Peak RF Power in Simultaneous Multi-Slice RF Excitation Pulses. Proc. ISMRM Annu. Meet. Exhib. (2012).
11. Conolly, S., Nishimura, D. & Macovski, A. Optimal Control Solutions to the Magnetic Resonance Selective Excitation Problem. IEEE Trans. Med. Imaging MI-5, 106–115 (1986).
12. Pauly, J., Le Roux, P., Nishimura, D. & Macovski, A. Parameter relations for the Shinnar-Le Roux selective excitation pulse design algorithm (NMR imaging). IEEE Trans. Med. Imaging 10, 53–65 (1991). 13. Setsompop, K. et al. High-resolution in vivo diffusion imaging of the human brain with generalized slice dithered enhanced resolution: Simultaneous multislice (gSlider-SMS). Magn. Reson. Med. 79, 141–151 (2018).
14. Sharma, A., Lustig, M. & Grissom, W. A. Root-flipped multiband refocusing pulses. Magn. Reson. Med. 75, 227–237 (2016).
15. Kerr, A. & Pauly, J. M. Slice Profile Stabilization for Segmented K-Space Magnetic Resonance Imaging. (1996).
16. Glover, G. H. Simple analytic spiral K-space algorithm. Magn. Reson. Med. 42, 412–5 (1999). 17. Kim, D., Adalsteinsson, E. & Spielman, D. M. Simple analytic variable density spiral design. Magn. Reson. Med. 50, 214–9 (2003).
18. Grissom, W. k-Space domain parallel transmit pulse design. Proc. ISMRM Annu. Meet. Exhib. (2018).
19. Xu, D., King, K. F., Zhu, Y., McKinnon, G. C. & Liang, Z.-P. Designing multichannel, multidimensional, arbitrary flip angle RF pulses using an optimal control approach. Magn. Reson. Med. 59, 547–60 (2008).
20. Grissom, W. A., Khalighi, M.-M., Sacolick, L. I., Rutt, B. K. & Vogel, M. W. Small-tip-angle spokes pulse design using interleaved greedy and local optimization methods. Magn. Reson. Med. 68, 1553–62 (2012).
21. Cao, Z., Donahue, M. J., Ma, J. & Grissom, W. A. Joint design of large-tip-angle parallel RF pulses and blipped gradient trajectories. Magn. Reson. Med. 75, 1198–208 (2016).
Figures