Problem 1

Part 1

No information about MAR.
MDR is 64 bits.

Part 2

7 bits are needed.
Largest positive number = 0111111 (63)
Largest unsigned number = 1111111 (127)

Part 3

Yes there is a problem. We will need 5 bits to represent each register. Add instruction takes 3 registers and needs a 4-bit opcode. Therefore we need at least 19 bits for the ADD instruction. However in the LC-2 ISA each instruction is only 16 bits.

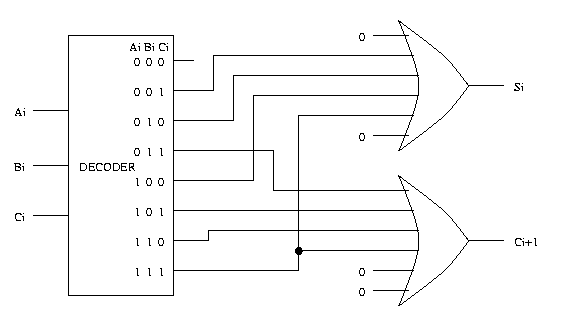
Problem 2

A B | C D Z
----|------
0 0 | 1 1 0
0 1 | 1 0 0
1 0 | 0 1 0
1 1 | 0 0 1

Z = A AND B

Problem 4

For the instruction whose opcode is 0001 (ADD):

	Fetch Instruction	Decode	Evaluate Address	Fetch Data	Execute	Store Result
PC	X
IR	X
MAR	X
MDR	X

For the instruction whose opcode is 0010 (LD):

	Fetch Instruction	Decode	Evaluate Address	Fetch Data	Execute	Store Result
PC	X
IR	X
MAR	X		X(a)	X(b)
MDR	X			X

There should be at least one checkmark in the two boxes marked (a), (b)

For the instruction whose opcode is 0011 (ST):

	Fetch Instruction	Decode	Evaluate Address	Fetch Data	Execute	Store Result
PC	X
IR	X
MAR	X		X(a)	X(b)	X(c)	X(d)
MDR	X			X(1)	X(2)	X(3)

There should be at least one checkmark in the boxes marked (a), (b), (c), (d)
There should be at least one checkmark in the boxes marked (1), (2), (3)

For the instruction whose opcode is 0000 (a control instruction):

	Fetch Instruction	Decode	Evaluate Address	Fetch Data	Execute	Store Result
PC	X				X
IR	X
MAR	X
MDR	X

Problem 4

Problem 5

(1): 1001 100 001 111111     ; R4 <- NOT(R1)

(2): 1001 101 010 111111     ; R5 <- NOT(R2)

(3): 0101 110 100 000 101    ; R6 <- R4 AND R5

(4): 1001 011 110 111111     ; R3 <- NOT(R6)

Problem 6

Sign	Exponent	Fraction
1	1 1 0 0	1 0 1


= -1^Sign x 2^{(Exponent - 7)} x 1.Fraction
= -1¹ x 2^{(12 - 7)} x 1.101
= -52

Problem 7

Part A:

M = 1, N = 1, P = 1

Part B:

E changes to 0