Instructions

Questions

1. The following data flow graph receives as inputs a value x, an n element vector V0, V1, ..., Vn-1, the value n, and a value 0 on its four input ports.

   

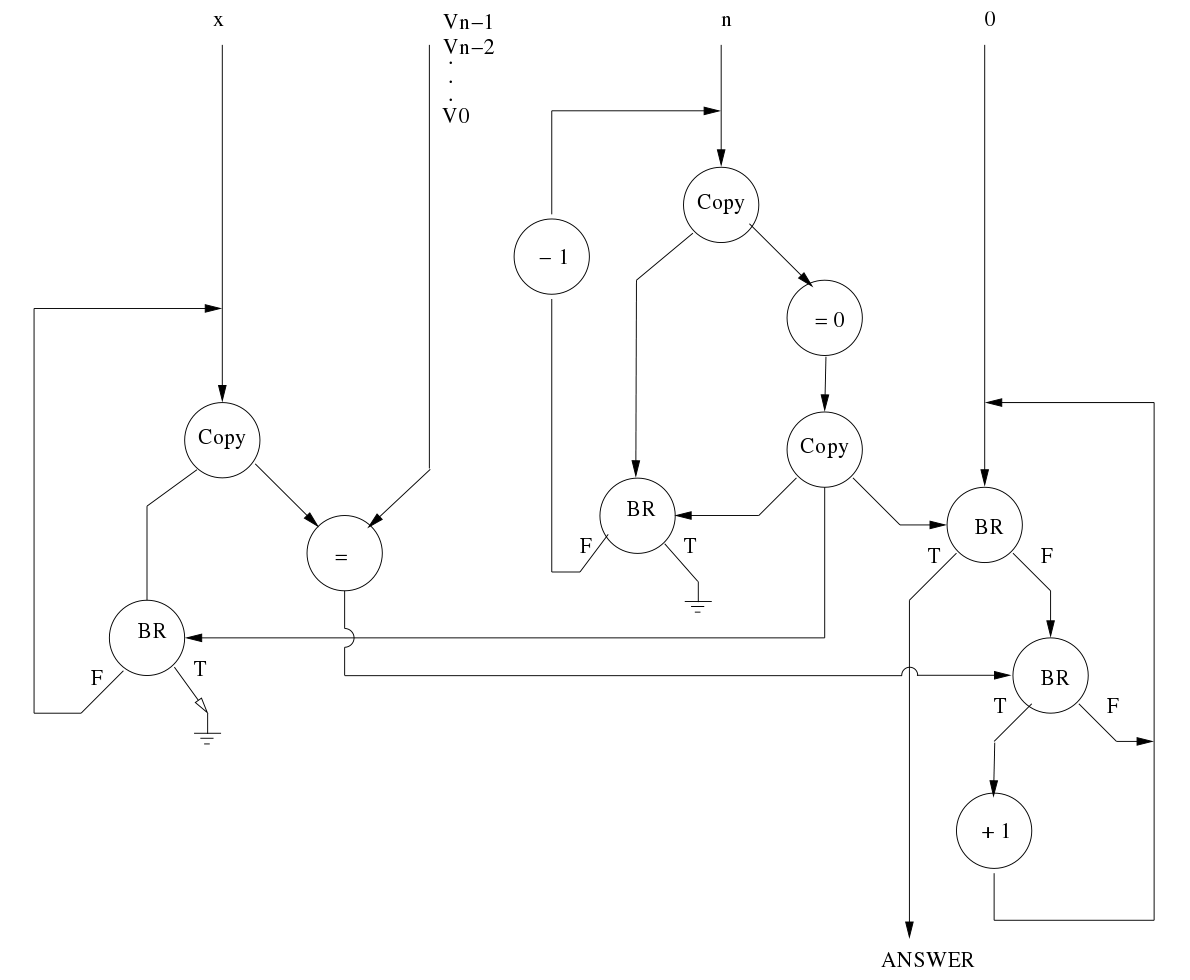
   What "answer" is produced by the execution of this data flow graph?

2. We must compute the following expression:

       a*x^6 + b*x^5 + c*x^4 + d*x^3 + e*x^2 + f*x + g 
   

   • How many operations and time-steps will the computation take on a single processor system (Use the smallest number of operations possible)?
   • How many operations and time-steps will the computation take on a multiprocessor system with 4 processors? (Use the smallest number of operations possible)
   • What is the speedup of the multiprocessor system over a single processor?

3. Speed-up with p processors is defined as T1/Tp, where T1 is the time to solve the problem with one processor and Tp is the time to solve the problem if you have p processors. What important requirement is there on T1?

4. Consider the following example used to explain Tomasulo's Algorithm:

   
   Format: Opcode Destination Source1 Source2
   MUL R3,  R1, R2
   ADD R5,  R3, R4
   ADD R7,  R2, R6
   ADD R10, R8, R9
   MUL R11, R7, R10
   ADD R5,  R5, R11
   MUL R10, R4, R10
   

   Construct the Data Flow Graph for this program.

5. In an Omega network as presented in class, assume that there are n inputs and n outputs. Let k be the size of each switch. For k taking the values 2, 4, 8, and 64, answer the following questions. (Assume the cost of each switch is k^2)

   1. What is the cost of the network as a function of n?
   2. What is the latency of the network?
   3. Assume that n=64. What k value would you choose? Why? State your assumptions and design point.

6. A four processor system, each processor having its own cache , uses the Directory scheme to maintain cache coherence. The directory stores a bit vector for each "line" (or, "block") of memory, indicating its status relative to the caches. Assume no cache has line A. Then in sequence: processor 1 wishes to read a value in line A, processor 2 wishes to write a value in line A, processor 3 wishes to read a value in line A. At the end of this sequence, what are the contents of the bit vector for line A.