Chapter 5: Expressions

What's in Chapter 5?

Most programming languages support the traditional concept of an expression as a combination of constants, variables, array elements, and function calls joined by various operators (+, -, etc.) to produce a single numeric value. Each operator is applied to one or two operands (the values operated on) to produce a single value which may itself be an operand for another operator. This idea is generalized in C by including nontraditional data types and a rich set of operators. Pointers, unsubscripted array names, and function names are allowed as operands. And, as Tables 5-1 through 5-6 illustrate, many operators are available. All of these operators can be combined in any useful manner in an expression. As a result, C allows the writing very compact and efficient expressions which at first glance may seem a bit strange. Another unusual feature of C is that anywhere the syntax calls for an expression, a list of expressions, with comma separators, may appear.

Precedence and associativity

The basic problem in evaluating expressions is deciding which parts of an expression are to be associated with which operators. To eliminate ambiguity, operators are given three properties: operand count, precedence, and associativity.

Operand count refers to the classification of operators as unary, binary, or ternary according to whether they operate on one, two, or three operands. The unary minus sign, for instance, reverses the sign of the following operand, whereas the binary minus sign subtracts one operand from another.

The following example converts the distance x in inches to a distance y in cm. Without parentheses the following statement seems ambiguous

If we divide first, then y can only take on values that are multiples of 254 (e.g., 0 254 508 etc.) So the following statement is incorrect.

The proper approach is to multiply first then divide. To multiply first we must guarantee that the product 254*x will not overflow the precision of the computer. How do we know what precision the compiler used for the intermediate result 254*x? To answer this question, we must observe the assembly code generated by the compiler. Since multiplication and division associate left to right, the first statement without parentheses although ambiguous will actually calculate the correct answer. It is good programming style to use parentheses to clarify the expression. So this last statement has both good style and proper calculation.

The issues of precedence and associativity were explained in Chapter 1. Precedence defines the evaluation order. For example the expression 3+4*2 will be 11 because multiplication as precedence over addition. Associativity determines the order of execution for operators that have the same precedence. For example, the expression 10-3-2 will be 5, because subtraction associates left to right. On the other hand, if x and y are initially 10, then the expression x+=y+=1 will first make y=y+1 (11), then make x=x+y (21) because the operator += associates right to left. The table from chapter 1 is repeated for your convenience.

Precedence	Operators	Associativity
highest	()  []  .  ->  ++(postfix)   --(postfix)	left to right
	++(prefix)  --(prefix)   !~ sizeof(type) +(unary)  -(unary) &(address) *(dereference)	right to left
	*   /   %	left to right
	+   -	left to right
	<<   >>	left to right
	<    <=   >   >=	left to right
	==  !=	left to right
	&	left to right
	^	left to right
	|	left to right
	&&	left to right
	||	left to right
	? :	right to left
	=   +=   -=  *=  /=  %=  <<=  >>=  |=  &=  ^=	right to left
lowest	,	left to right

Table 1-4: Precedence and associativity determine the order of operation

Unary operators

We begin with the unary operators, which take a single input and give a single output. In the following examples, assume all numbers are 16 bit signed (short). The following variables are listed
short data; /* -32767 to +32767 */
short *pt;  /* pointer to memory */
short flag; /* 0 is false, not zero is true */

operator	meaning	example	result
~	binary complement	~0x1234	0xEDCB
!	logical complement	!flag	flip 0 to 1 and notzero to 0
&	address of	&data	address in memory where data is stored
-	negate	-100	negative 100
+	positive	+100	100
++	preincrement	++data	data=data+1, then result is data
--	predecrement	--data	data=data-1, then result is data
*	reference	*pt	16 bit information pointed to by pt

operator	meaning	example	result
++	postincrement	data++	result is data, then data=data+1
--	postdecrement	data--	result is data, then data=data+1

Binary operators

Next we list the binary arithmetic operators, which operate on two number inputs giving a single number result. The operations of addition, subtraction and shift left are the same independent of whether the numbers are signed or unsigned. As we will see later, overflow and underflow after an addition, subtraction and shift left are different for signed and unsigned numbers, but the operation itself is the same. On the other hand multiplication, division, and shift right have different functions depending on whether the numbers are signed or unsigned. It will be important, therefore, to avoid multiplying or dividing an unsigned number with a signed number.

operator	meaning	example	result
+	addition	100+300	400
-	subtraction	100-300	-200
*	multiplication	10*300	3000
/	division	123/10	12
%	remainder	123%10	3
<<	shift left	102<<2	408
>>	shift right	102>>2	25

The binary bitwise logical operators take two inputs and give a single result.

operator	meaning	example	result
&	bitwise and	0x1234&0x00FF	0x0034
|	bitwise or	0x1234|0x00FF	0x12FF
^	bitwise exclusive or	0x1234^0x00FF	0x12CB

The binary Boolean operators take two Boolean inputs and give a single Boolean result.

operator	meaning	example	result
&&	and	0 && 1	0 (false)
||	or	0 || 1	1 (true)

Many programmers confuse the logical operators with the Boolean operators. Logical operators take two numbers and perform a bitwise logical operation. Boolean operators take two Boolean inputs (0 and notzero) and return a Boolean (0 or 1). In the program below, the operation c=a&b; will perform a bitwise logical and of 0x0F0F and 0xF0F0 resulting in 0x0000. In the d=a&&b; expression, the value a is considered as a true (because it is not zero) and the value b also is considered a true (not zero). The Boolean operation of true and true gives a true result (1).
short a,b,c,d;
int main(void){ a=0x0F0F; b=F0F0;
  c = a&b;  /* logical result c will be 0x0000 */
  d = a&&b; /* Boolean result d will be 1 (true) */
  return 1;
}

Listing 5-1: Illustration of the difference between logical and Boolean operators

The binary relational operators take two number inputs and give a single Boolean result.

operator	meaning	example	result
==	equal	100 == 200	0 (false)
!=	not equal	100 != 200	1 (true)
<	less than	100 < 200	1 (true)
<=	less than or equal	100 <= 200	1 (true)
>	greater than	100 > 200	0 (false)
>=	greater than or equal	100 >= 200	0 (false)

Some programmers confuse assignment equals with the relational equals. In the following example, the first if will execute the subfunction() if a is equal to zero (a is not modified). In the second case, the variable b is set to zero, and the subfunction() will never be executed because the result of the equals assignment is the value (in this case the 0 means false).
short a,b;
void program(void){
  if(a==0) subfunction(); /* execute subfunction if a is zero */
  if(b=0) subfunction();  /* set b to zero, never execute subfunction */
}

Listing 5-2: Illustration of the difference between relational and assignment equals

Before looking at the kinds of expressions we can write in C, we will first consider the process of evaluating expressions and some general properties of operators.

Assignment Operators

The assignment operator is used to store data into variables. The syntax is variable=expression; where variable has been previously defined. At run time, the result of the expression is saved into the variable. If the type of the expression is different from the variable, then the result is automatically converted. For more information about types and conversion, see expression type and explicit casting. The assignment operation itself has a result, so the assignment operation can be nested.
short a,b;
void initialize(void){
  a = b = 0; /* set both variables to zero */
}

Listing 5-3: Example of a nested assignment operation

The read/modify write assignment operators are convenient. Examples are shown below.
short a,b;
void initialize(void){
    a += b;  /* same as a=a+b */
    a -= b;  /* same as a=a-b */
    a *= b;  /* same as a=a*b */
    a /= b;  /* same as a=a/b */
    a %= b;  /* same as a=a%b */
    a <<= b; /* same as a=a<<b */
    a <<= b; /* same as a=a<<b */
    a >>= b; /* same as a=a>>b */
    a |= b;  /* same as a=a|b */
    a &= b;  /* same as a=a&b */
    a ^= b;  /* same as a=a^b */
}

Listing 5-4 List of all read/modify/write assignment operations

Most compilers will produce the same code for the short and long version of the operation. Therefore you should use the read/modify/write operations only in situations that make the software easier to understand.
void function(void){
  PORTA |= 0x01;  /* set PA0 high */
  PORTB &=~ 0x80; /* clear PB7 low */
  PORTC ^= 0x40;  /* toggle PC6 */
}

Listing 5-5 Good examples of read/modify/write assignment operations

Expression Types and Explicit Casting

We saw earlier that numbers are represented in the computer using a wide range of formats. A list of these formats is given in Table 5.7. Notice that for the Cortex M, the int and long types are the same. On the other hand with the Freescale 9S12, the int and short types are the same. This difference may cause confusion, when porting code from one system to another. I suggest you use the int type when you are interested in efficiency and don't care about precision, and use the short type when you want a variable with a 16-bit precision.

type	range	precision	example variable
unsigned char	0 to 255	8 bits	unsigned char uc;
char	-128 to 127	8 bits	char sc;
unsigned int	0 to 4294967295	32 bits	unsigned int ui;
int	-2147483648 to 2147483647	32 bits	int si;
unsigned short	0 to 65535U	16 bits	unsigned short us;
short	-32768 to 32767	16 bits	short ss;
long	-2147483648 to 2147483647	32 bits	long sl;
unsigned long	0 to 4294967295	32 bits	unsigned long ui;

An obvious question arises, what happens when two numbers of different types are operated on? Before operation, the C compiler will first convert one or both numbers so they have the same type. The conversion of one type into another has many names:
  automatic conversion,
  implicit conversion,
  coercion,
  promotion, or
  widening.

There are three ways to consider this issue. The first way to think about this is if the range of one type completely fits within the range of the other, then the number with the smaller range is converted (promoted) to the type of the number with the larger range. In the following examples, a number of type1 is added to a number of type2. In each case, the number range of type1 fits into the range of type2, so the parameter of type1 is first promoted to type2 before the addition.

type1		type2	example
unsigned char	fits inside	unsigned short	uc+us is of type unsigned short
unsigned char	fits inside	short	uc+ss is of type short
unsigned char	fits inside	long	uc+sl is of type long
char	fits inside	short	sc+ss is of type short
char	fits inside	long	sc+sl is of type long
unsigned short	fits inside	long	us+sl is of type long
short	fits inside	long	ss+sl is of type long

The second way to consider mixed precision operations is that in most cases the compiler will promote the number with the smaller precision into the other type before operation. If the two numbers are of the same precision, then the signed number is converted to unsigned. These automatic conversions may not yield correct results. The third and best way to deal with mixed type operations is to perform the conversions explicitly using the cast operation. We can force the type of an expression by explicitly defining its type. This approach allows the programmer to explicitly choose the type of the operation. Consider the following digital filter with mixed type operations. In this example, we explicitly convert x and y to signed 16 bit numbers and perform 16 bit signed arithmetic. Note that the assignment of the result into y, will require a demotion of the 16 bit signed number into 8 bit signed. Unfortunately, C does not provide any simple mechanisms for error detection/correction (see overflow and underflow.)

char y; // output of the filter
unsigned char x; // input of the filter
void filter(void){
  y = (12*(short)x + 56*(short)y)/100;
}

Listing 5-6: Examples of the selection operator

We apply an explicit cast simply by preceding the number or expression with parentheses surrounding the type. In this next digital filter all numbers are of the same type. Even so, we are worried that the intermediate result of the multiplications and additions might overflow the 16-bit arithmetic. We know from digital signal processing that the final result will always fit into the 16-bit variable. For more information on the design and analysis of digital filters,  see Chapter 5 of Embedded Systems: Real-Time Operating Systems for ARM Cortex M Microcontrollers by Jonathan W. Valvano. In this example, the cast (long) will specify the calculations be performed in 32-bit precision.

// y(n) = [113*x(n) + 113*x(n-2) - 98*y(n-2)]/128, channel specifies the A/D channel
short x[3],y[3]; // MACQs containing current and previous
void SysTick_Handler(void){
  y[2]=y[1]; y[1]=y[0]; // shift MACQ
  x[2]=x[1]; x[1]=x[0];
  x[0] = A2D(channel); // new data
  y[0] = (113*((long)x[0]+(long)x[2])-98*(long)y[2])>>7;}

Listing 5-7: We can use a cast to force higher precision arithmetic

We saw in Chapter 1, casting was used to assign a symbolic name to an I/O port. In particular the following define casts the number 0x400043FC as a pointer type, which points to an unsigned 32-bit data. More about pointers can be found in Chapter 7.

#define GPIO_PORTA_DATA_R (*((volatile unsigned long *)0x400043FC))


Selection operator

The selection operator takes three input parameters and yields one output result. The format is

The first input parameter is an expression, Expr1, which yields a boolean (0 for false, not zero for true). Expr2 and Expr3 return values that are regular numbers. The selection operator will return the result of Expr2 if the value of Expr1 is true, and will return the result of Expr3 if the value of Expr1 is false. The type of the expression is determined by the types of Expr2 and Expr3. If Expr2 and Expr3 have different types, then the usual promotion is applied. The resulting time is determined at compile time, in a similar manner as the Expr2+Expr3 operation, and not at run time depending on the value of Expr1. The following two subroutines have identical functions.
short a,b;
void sub1(void){
  a = (b==1) ? 10 : 1;
}
void sub2(void){
  if(b==1)
     a=10;
  else
     a=1; 
}

Listing 5-8: Examples of the selection operator

Arithmetic Overflow and Underflow

An important issue when performing arithmetic calculations on integer values is the problem of underflow and overflow. Arithmetic operations include addition, subtraction, multiplication, division and shifting. Overflow and underflow errors can occur during all of these operations. In assembly language the programmer is warned that an error has occurred because the processor will set condition code bits after each of these operations. Unfortunately, the C compiler provides no direct access to these error codes, so we must develop careful strategies for dealing with overflow and underflow. It is important to remember that arithmetic operations (addition, subtraction, multiplication, division, and shifting) have constraints when performed with finite precision on a microcomputer. An overflow error occurs when the result of an arithmetic operation can not fit into the finite precision of the result. We will study addition and subtraction operations in detail, but the techniques for dealing with overflow and underflow will apply to the other arithmetic operations as well. We will consider two approaches

For example when two 8 bit numbers are added, the sum may not fit back into the 8 bit result. We saw earlier that the same digital hardware (instructions) could be used to add and subtract unsigned and signed numbers. Unfortunately, we will have to design separate overflow detection for signed and unsigned addition and subtraction.

All microcomputers have a condition code register which contain bits which specify the status of the most recent operation. In this section, we will introduce 4 condition code bits common to most microcomputers. If the two inputs to an addition or subtraction operation are considered as unsigned, then the C bit (carry) will be set if the result does not fit. In other words, after an unsigned addition, the C bit is set if the answer is wrong. If the two inputs to an addition or subtraction operation are considered as signed, then the V bit (overflow) will be set if the result does not fit. In other words, after a signed addition, the V bit is set if the answer is wrong. The Freescale 6805 does not have a V bit, therefore it will be difficult to check for errors after an operation on signed numbers.

bit  name        meaning after addition or subtraction
N    negative    result is negative
Z    zero        result is zero
V    overflow    signed overflow
C    carry       unsigned overflow

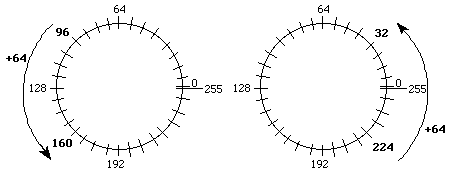
For an 8 bit unsigned number, there are only 256 possible values, 0 to 255. We can think of the numbers as positions along a circle. There is a discontinuity at the 0|255 interface, everywhere else adjacent numbers differ by ±1. If we add two unsigned numbers, we start at the position of the first number a move in a clockwise direction the number of steps equal to the second number. For example, if 96+64 is performed in 8 bit unsigned precision, the correct result of 160 is obtained. In this case, the carry bit will be 0 signifying the answer is correct. On the other hand, if 224+64 is performed in 8 bit unsigned precision, the incorrect result of 32 is obtained. In this case, the carry bit will be 1, signifying the answer is wrong.

Figure 5-1: 8 bit unsigned addition.

For subtraction, we start at the position of the first number a move in a counterclockwise direction the number of steps equal to the second number. For example, if 160-64 is performed in 8 bit unsigned precision, the correct result of 96 is obtained (carry bit will be 0.) On the other hand, if 32-64 is performed in 8 bit unsigned precision, the incorrect result of 224 is obtained (carry bit will be 1.)

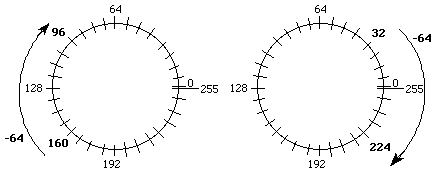
Figure 5-2: 8 bit unsigned subtraction.

In general, we see that the carry bit is set when we cross over from 255 to 0 while adding or cross over from 0 to 255 while subtracting.

Observation: The carry bit, C, is set after an unsigned add or subtract when the result is incorrect.

For an 8 bit signed number, the possible values range from -128 to 127. Again there is a discontinuity, but this time it exists at the -128|127 interface, everywhere else adjacent numbers differ by ±1. The meanings of the numbers with bit 7=1 are different from unsigned, but we add and subtract signed numbers on the number wheel in a similar way (e.g., addition of a positive number moves clockwise.) Adding a negative number is the same as subtracting a positive number hence this operation would cause a counterclockwise motion. For example, if -32+64 is performed, the correct result of 32 is obtained. In this case, the overflow bit will be 0 signifying the answer is correct. On the other hand, if 96+64 is performed, the incorrect result of -96 is obtained. In this case, the overflow bit will be 1 signifying the answer is wrong.

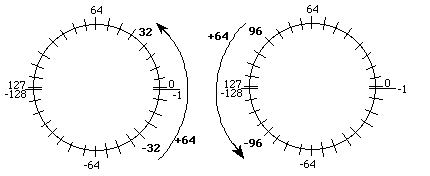
Figure 5-3: 8 bit signed addition.

For subtracting signed numbers, we again move in a counterclockwise direction. Subtracting a negative number is the same as adding a positive number hence this operation would cause a clockwise motion. For example, if 32-64 is performed, the correct result of -32 is obtained (overflow bit will be 0.) On the other hand, if -96-64 is performed, the incorrect result of 96 is obtained (overflow bit will be 1.)

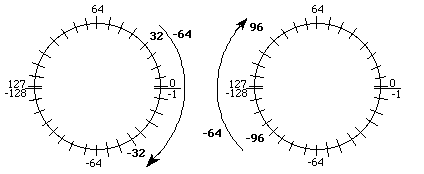
Figure 5-4: 8 bit signed subtraction.

In general, we see that the overflow bit is set when we cross over from 127 to -128 while adding or cross over from -128 to 127 while subtracting.

Observation: The overflow bit, V, is set after a signed add or subtract when the result is incorrect.

Another way to determine the overflow bit after an addition is to consider the carry out of bit 6. The V bit will be set of there is a carry out of bit 6 (into bit 7) but no carry out of bit 7 (into the C bit). It is also set if there is no carry out of bit 6 but there is a carry out of bit 7. Let X7,X6,X5,X4,X3,X2,X1,X0 and M7,M6,M5,M4,M3,M2,M1,M0 be the individual binary bits of the two 8 bit numbers which are to be added, and let R7,R6,R5,R4,R3,R2,R1,R0 be individual binary bits of the 8 bit sum. Then, the 4 condition code bits after an addition are shown in Table 5.10.

Let the result R be the result of the subtraction X-M. Then, the 4 condition code bits are shown in Table 5.11.

Common Error: Ignoring overflow (signed or unsigned) can result in significant errors.

Observation: Microcomputers have two sets of conditional branch instructions (if statements) which make program decisions based on either the C or V bit.

Common Error: An error will occur if you unsigned conditional branch instructions (if statements) after operating on signed numbers, and vice-versa.

There are some applications where arithmetic errors are not possible. For example if we had two 8 bit unsigned numbers that we knew were in the range of 0 to 100, then no overflow is possible when they are added together.

Typically the numbers we are processing are either signed or unsigned (but not both), so we need only consider the corresponding C or V bit (but not both the C and V bits at the same time.) In other words, if the two numbers are unsigned, then we look at the C bit and ignore the V bit. Conversely, if the two numbers are signed, then we look at the V bit and ignore the C bit. There are two appropriate mechanisms to deal with the potential for arithmetic errors when adding and subtracting. The first mechanism, used by most compilers, is called promotion. Promotion involves increasing the precision of the input numbers, and performing the operation at that higher precision. An error can still occur if the result is stored back into the smaller precision. Fortunately, the program has the ability to test the intermediate result to see if it will fit into the smaller precision. To promote an unsigned number we add zero’s to the left side. In a previous example, we added the unsigned 8 bit 224 to 64, and got the wrong result of 32. With promotion we first convert the two 8 bit numbers to 16 bits, then add.

We can check the 16 bit intermediate result (e.g., 228) to see if the answer will fit back into the 8 bit result. In the following flowchart, X and M are 8 bit unsigned inputs, X16, M16, and R16 are 16 bit intermediate values, and R is an 8 bit unsigned output. The oval symbol represents the entry and exit points, the rectangle is used for calculations, and the diamond shows a decision. Later in the book we will use parallelograms and trapezoids to perform input/output functions.

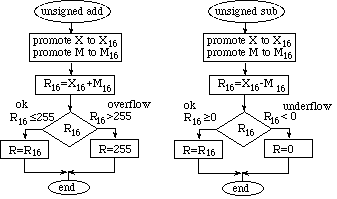
To promote a signed number, we duplicate the sign bit as we add binary digits to the left side. Earlier, we performed the 8 bit signed operation -96-64 and got a signed overflow. With promotion we first convert the two numbers to 16 bits, then subtract.

We can check the 16 bit intermediate result (e.g., -160) to see if the answer will fit back into the 8 bit result. In the following flowchart, X and M are 8 bit signed inputs, X16, M16, and R16 are 16 bit signed intermediate values, and R is an 8 bit signed output.

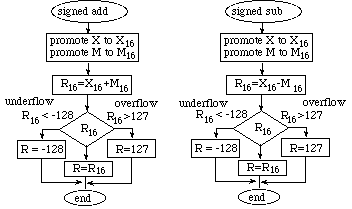
The other mechanism for handling addition and subtraction errors is called ceiling and floor. It is analogous to movements inside a room. If we try to move up (add a positive number or subtract a negative number) the ceiling will prevent us from exceeding the bounds of the room. Similarly, if we try to move down (subtract a positive number or add a negative number) the floor will prevent us from going too low. For our 8 bit addition and subtraction, we will prevent the 0 to 255 and 255 to 0 crossovers for unsigned operations and -128 to +127 and +127 to -128 crossovers for signed operations. These operations are described by the following flowcharts. If the carry bit is set after an unsigned addition the result is adjusted to the largest possible unsigned number (ceiling). If the carry bit is set after an unsigned subtraction, the result is adjusted to the smallest possible unsigned number (floor.)

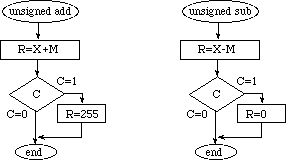
If the overflow bit is set after a signed operation the result is adjusted to the largest (ceiling) or smallest (floor) possible signed number depending on whether it was a -128 to 127 cross over (N=0) or 127 to -128 cross over (N=1). Notice that after a signed overflow, bit 7 of the result is always wrong because there was a cross over.

Go to Chapter 6 on Statements Return to Table of Contents