Chapter 4: Finite State Machines

Jonathan Valvano and Ramesh Yerraballi

 

Time is a critical parameter in an embedded system. In this chapter, we will further develop SysTick as a means to control time in our embedded system. We will activate the phase-lock-loop (PLL) for two reasons. First, by selecting the bus frequency we can trade-off power for speed. Second, by creating a bus clock based on an external crystal, system time will be very accurate. An effective development process will be to separate what the system does from how it works. This abstraction will be illustrated during the design of finite state machines (FSM). All embedded systems have inputs and outputs, but FSMs have states. We will embody knowledge, “what we know” or “where we’ve been”, by being in a state.  A traffic light and vending machine will be implemented using FSMs. Finally, we will introduce stepper motors and show how to use a FSM to control the motors.

 

Table of Contents:

• 4.1. Performance/Power Trade-off
• 4.2. Accurate Time Delays using SysTick
• 4.3. Structures
  
• 4.4. Finite State Machines with Indexed Structures
  
•         Traffic Light Controller
  
•         Vending Machine Controller
  
• 4.5. Stepper Motors
  

Return to book table of contents

 

Video 4.0. Introduction to FSM

 

4.1. Performance/Power Trade-off

Video 4.1.1. Software performance **needs recording**

We can make a first order estimate of the relationship between work done in the software and electrical power required to run the system. There are two factors involved in the performance of software: efficiency of the software and the number of instructions being executed per second

       Software Work = algorithm * instructions/sec

In other words, if we want to improve software performance we can write better software or increase the rate at which we execute instructions. Recall that the compiler converts our C software into Cortex M machine code, so the efficiency of the compiler will also affect this relationship. Furthermore, most compilers have optimization settings that allow you to make your software run faster at the expense of using more memory. On the Cortex M, most instructions execute in 1 or 2 bus cycles. In CMOS logic, most of the electrical power required to run the system occurs in making signals change. It takes power to make a digital signal rise from 0 to 1, or fall from 1 to 0. It takes some power to run independent of frequency. Figure 4.1.1 shows the supply current as a function of frequency for the MSPM0G3507 microcontroller. Simplifying things greatly, we see a simple and linear relationship between bus frequency and supply current to the MSPM0G3507. Notice in Figure 4.1.1 that m=0.0817mA/MHz is the slope of this linear relationship.

       I_cc = m * f_Bus

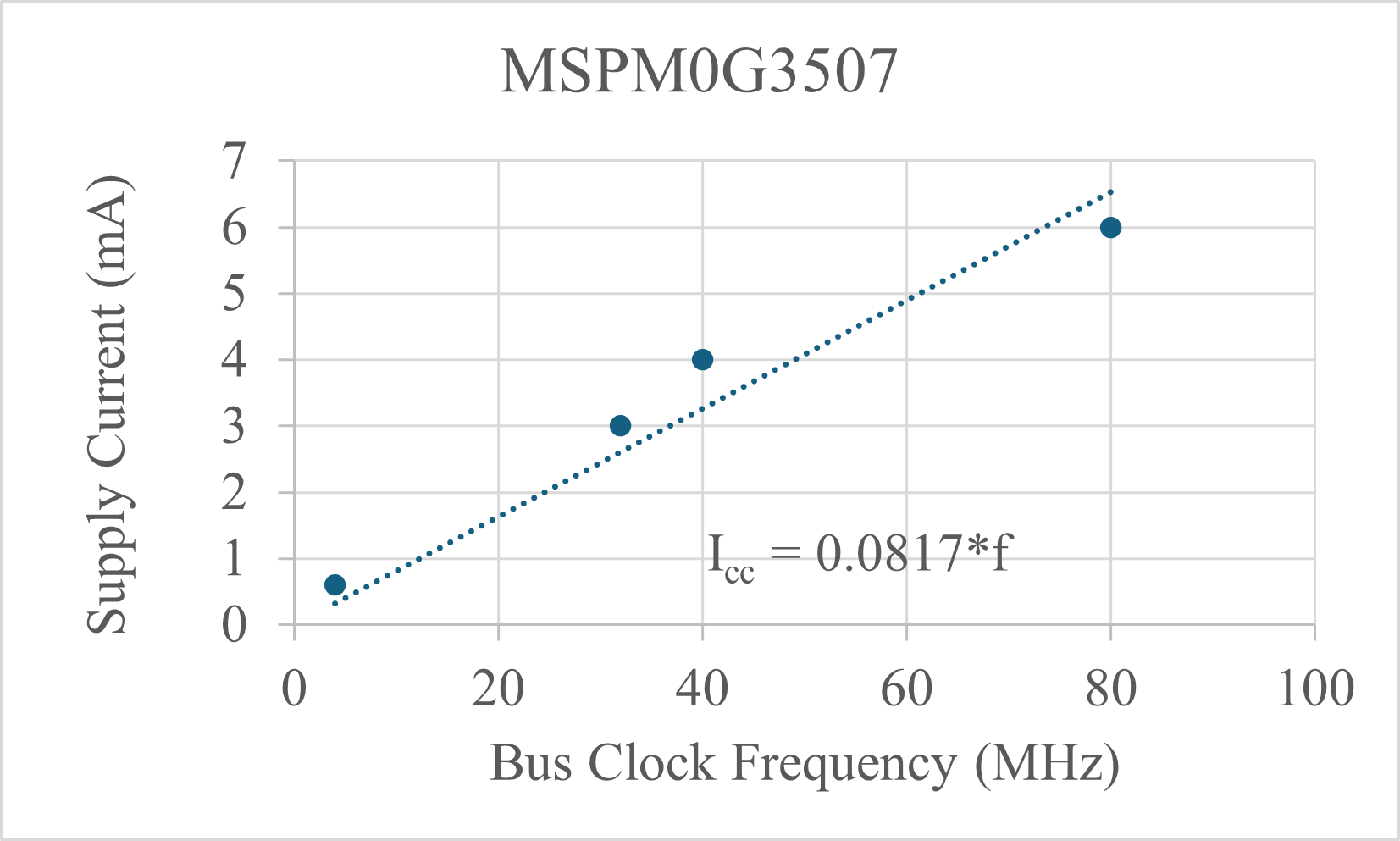
Figure 4.1.1. CMOS logic exhibits a linear relationship between supply current and bus clock frequency.

If the processor is running at V_cc, then the electrical power will be

       Power = I_cc * V_cc

Some of the factors that affect the slope m are operating voltage and fundamental behavior of how the CMOS transistors are designed. If we approximate the Cortex M processor as being able to execute one instruction every two bus cycles, we can combine the above two equations to see the speed-power trade-off.

       Software Work = algorithm * ½ f_Bus = algorithm * ½ Power/m

Observation: To save power, we slow down the bus frequency removing as much of the wasted bus cycles while still performing all of the required tasks.

For battery-powered systems the consumed power is a critical factor. For these systems we need to measure power. Since there are so many factors that determine power, the data sheets for the devices will only be approximate. Since power equals voltage times current, and we know the voltage (in our case 3.3V), we need to measure supply current. Figure 4.1.2 shows a current sense amplifier that can measure current to a Target system. We made a special printed circuit board placing a fixed resistor (R1=1 ohm in this circuit) between the 3.3V supply and the target system. The voltage across R1 is a linear function of the current to the target. The current sense amplifier (LT1187) amplifies this signal and the output of the amplifier is measured by an analog to digital converter.   

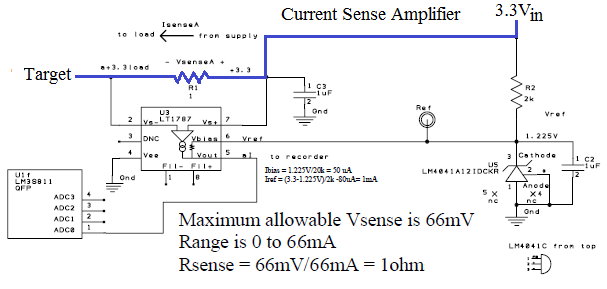
Figure 4.1.2. A current sense amplifier can be used to measure instantaneous current to the target. The blue trace shows the current path from supply to target.

Figure 4.1.3 shows a current measurement for a battery-powered system. In sleep mode all the clocks are turned off and the current drops to less than 1 µA. The MSPM0 software has control over which I/O devices are active. You can see from the data, the I/O devices are turned on one at a time (sample from ADC, transmit using RF, and receive using RF). The total energy needed to collect one measurement on this system can be found by multiplying current*voltage*time, where current and time are measured in Figure 4.1.3. In this calculation, assume we take on measurement every hour (sleeps for 1 hour, wakes up samples, transmits, receives, and then goes back to sleep).

    (14mA*0.005s+31mA*0.007s+21mA*0.0046s+0.001mA*3600s)*3.3V/hr = 0.0013J/hr

A 3.3V battery with 100mA-hr has 0.33J of energy. This battery will run the system for  0.33J/0.0013J/hr = 25 hours 

 

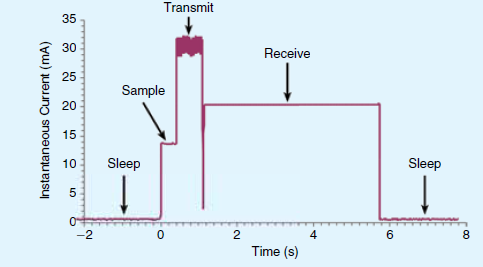
Figure 4.1.3. Instantaneous current measured on a battery powered system.

Checkpoint 4.1.1: Why is it important to control bus frequency in a low power design?

Checkpoint 4.1.2: Why would we turn off I/O ports if they are not needed?

Checkpoint 4.1.3: What does your cell-phone do when its battery level is low?

 

Quiz 4.1

Grade Quiz

 

4.2. Accurate Time Delays using SysTick

Video 4.2. SysTick for Accurate Delays***needs recording***

The accuracy of SysTick depends on the accuracy of the clock. We use the PLL to derive a bus clock based on the 40 MHz crystal, the time measured or generated using SysTick will be very accurate. More specifically, the accuracy of the crystal on the LaunchPad board is ±50 parts per million (PPM), which translates to 0.005%, which is about ±5 seconds per day. Most crystals are made with Silicon-dioxide Si-O₂ or silicon-oxygen tetrahedron Si-O₄. The frequency at which it resonants depends on its physical size/orientation/mass, which is constant, and not dependent on external factors like time and temperature. One could spend more money on the crystal and improve the accuracy by a factor of 10. Not only are crystals accurate, they are stable. The crystal will vary only ±150 PPM as temperature varies from -40 to +150 ºC. Crystals are more stable than they are accurate, typically varying by less than 5 PPM per year. For more information https://en.wikipedia.org/wiki/Crystal_oscillator

Program 4.2.1 shows a simple function to implement time delays based on SysTick. The LOAD register is set to the number of bus cycles one wishes to wait. If the PLL function has been executed, then the units of this delay will be 12.5 ns. Writing to VAL will clear the counter and will clear the count flag (bit 16) of the CTRL register. After SysTick has been decremented delay times, the count flag will be set and the while loop will terminate. Since SysTick is only 24 bits, the maximum time one can wait with SysTick_Wait is 2²⁴*12.5ns, which is about 200 ms. To provide for longer delays, the function SysTick_Wait10ms calls the function SysTick_Wait repeatedly. Notice that 800,000*12.5ns is 10ms.

void SysTick_Init(void){

  SysTick->CTRL = 0x00000005;      // enable SysTick with core clock

}

// The delay parameter is in units of the 80 MHz core clock. (12.5 ns)

void SysTick_Wait(uint32_t delay){

  SysTick->LOAD = delay-1;  // number of counts to wait

  SysTick->VAL = 0;        // any value written to VAL clears

  while((SysTick->CTRL&0x00010000)==0){ // wait for count flag

  }

}

// 800000*12.5ns equals 10ms

void SysTick_Wait10ms(uint32_t delay){

  uint32_t i;

  for(i=0; i<delay; i++){

    SysTick_Wait(800000);  // wait 10ms

  }

}

Program 4.2.1. Use of SysTick to delay for a specified amount of time .

Checkpoint 4.2.1: What is the longest time one could wait using SysTick_Wait10ms?

Checkpoint 4.2.2: How would you change Program 4.2.1 if the bus frequency were 32 MHz?

Video 4.2.1. Using SysTick to measure elapsed time ***needs recording***

 

Quiz 4.2

Grade Quiz

 

4.3. Structures

Video 4.3.1. Structs in C

A structure hashas elements with different types and/or precisions. In C, we use struct to define a structure. The const modifier causes the structure to be allocated in ROM. Without the const, the C compiler will place the structure in RAM, allowing it to be dynamically changed. If the structure were to contain an ASCII string of variable length, then we must allocate space to handle its maximum size. In this first example, the structure will be allocated in RAM so no const is included. The following code defines a structure with three elements. We give separate names to each element. In this example the elements are Xpos Ypos Score. The typedef command creates a new data type based on the structure, but no memory is allocated.

struct player{

  uint8_t Xpos;     // first element

  uint8_t Ypos;     // second element

  uint16_t Score;   // third element

};

typedef struct player player_t;

 

We can allocate a variable called Sprite of this type, which will occupy four bytes in RAM:

player_t Sprite;

 

We can access the individual elements of this variable using the syntax name.element. After these three lines are executed we have the data structure as shown in Figure 4.3.1 (assuming the variable occupies the four bytes starting at 0x2000.0250.

   Sprite.Xpos = 10;

   Sprite.Ypos = 20;

   Sprite.Score = 12000;

 

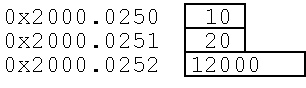
Figure 4.3.1. A structure collects elements of different sizes and/or types into one object.

We can also have an array of structures. We define structure array in a similar way as other arrays

player_t Ships[10];

uint32_t i;

 

While we are accessing an array, we must make sure the index is valid. In this case, the variable i must be between 0 and 9. We can read and write the individual fields using the syntax combining array access and structure access.

    Ships[i].Xpos = 10;

    Ships[i].Ypos = 20;

    Ships[i].Score = 12000;

 

The C function in Program 4.3.1 takes a player, moves it to location 50,50 and adds one point. For example, we execute  MoveCenter(6); to move the 7th ship to location 50,50 and increase its score.

// move to center and add to score

void MoveCenter(uint32_t i){

  Ships[i].Xpos = 50;

  Ships[i].Ypos = 50;

  if(Ships[i].Score < 65535){

    Ships[i].Score++;

  }

}

Program 4.3.1. A function that accesses a structure.

Observation: On the Cortex M0 the compiler must align 16-bit elements within structures to an even address and must align 32-bit elements to a word-aligned address.

Checkpoint 4.3.1: Think about the variable Sprite created with the player_t type. Assume the first entry Sprite.Xpos is word aligned. Can the compiler assign the three fields Sprite.Xpos, Sprite.Ypos, Sprite.Score contiguously in memory? Or, will it need to skip some bytes between Sprite.Ypos and Sprite.Score?

Checkpoint 4.3.2: Think about this structure struct thing{ int8_t x; int16_t z;}; What must the compiler do when allocating space in memory for this thing?

Without the const, the C compiler will place the structure in RAM, allowing it to be dynamically changed. If the structure resides in RAM, then the system will have to initialize the data structure explicitly by executing software. If the structure is in ROM, we must initialize it at compile time. The next section shows examples of ROM-based structures.

 

Quiz 4.3

Grade Quiz

 

4.4. Finite State Machines with Indexed Structures

A State Transition Graph (STG) has nodes and edges, where the nodes relate to the states of the FSM and the edges represent the transitions from one state to another when a particular input is received. Edges are accordingly labeled with the input that caused the transition. The output can also be captured in the Graph. Note that a FSM where the output is only dependent on the current state and not the input is called a Moore FSM.  FSMs where the output is dependent on both the current state and the input are called Mealy FSMs i.e.,

We note that some systems lend themselves better to a Mealy description while others are more naturally expressed as Moore machines. However, both machine descriptions are equivalent in that any system that can be described using a Mealy machine can also be expressed equivalently as a Moore machine and vice versa.  See Figure 5.5. 

Video 4.4.1. Introduction to FSMs

The FSM controller employs a well-defined model or framework with which we solve our problem. STG will be specified using either a linked or table data structure. An important aspect of this method is to create a 1-1 mapping from the STG into the data structure. The three advantages of this abstraction are 1) it can be faster to develop because many of the building blocks preexist; 2) it is easier to debug (prove correct) because it separates conceptual issues from implementation; and 3) it is easier to change. 

When designing a FSM, we begin by defining what constitutes a state. In a simple system like a single intersection traffic light, a state might be defined as the pattern of lights (i.e., which lights are on and which are off). In a more sophisticated traffic controller, what it means to be in a state might also include information about traffic volume at this and other adjacent intersections. The next step is to make a list of the various states in which the system might exist. As in all designs, we add outputs so the system can affect the external environment, and inputs so the system can collect information about its environment or receive commands as needed. The execution of a Moore FSM repeats this sequence over and over

            1. Perform output, which depends on the current state

            2. Wait a prescribed amount of time (optional)

            3. Input

            4. Go to next state, which depends on the input and the current state

 

The execution of a Mealy FSM repeats this sequence over and over

            1. Wait a prescribed amount of time (optional)

            2. Input

            3. Perform output, which depends on the input and the current state

            4. Go to next state, which depends on the input and the current state

 

There are other possible execution sequences. Therefore, it is important to document the sequence before the state graph is drawn. The high-level behavior of the system is defined by the state graph. The states are drawn as circles. Descriptive states names help explain what the machine is doing. Arrows are drawn from one state to another, and labeled with the input value causing that state transition.

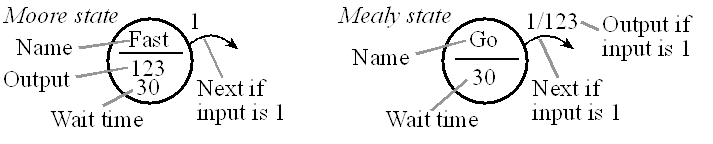
Figure 4.4.1. The output in a Moore depends just on the state. In a Mealy the output depends on state and input.

Observation: If the machine is such that a specific output value is necessary “to be a state”, then a Moore implementation will be more appropriate.

Observation: If the machine is such that no specific output value is necessary “to be a state”, but rather the output is required to transition the machine from one state to the next, then a Mealy implementation will be more appropriate.

A linked structure consists of multiple identically-structured nodes. Each node of the linked structure defines one state. One or more of the entries in the node is a link to other nodes. In an embedded system, we usually use statically-allocated fixed-size linked structures, which are defined at compile time and exist throughout the life of the software. In a simple embedded system the state graph is fixed, so we can store the linked data structure in nonvolatile memory. For complex systems where the control functions change dynamically (e.g., the state graph itself varies over time), we could implement dynamically-allocated linked structures, which are constructed at run time and number of nodes can grow and shrink in time. We will use a table structure to define the state graph, which consists of contiguous multiple identically-structured elements. Each element of the table defines one state. One or more of the entries is an index to other elements. The index is essentially a link to another state. An important factor when implementing FSMs is that there should be a clear and one-to-one mapping between the FSM state graph and the data structure. I.e., there should be one element of the structure for each state. If each state has four arrows, then each node of the linked structure should have four links.

The outputs of Moore FSM are only a function of the current state. In contrast, the outputs are a function of both the input and the current state in a Mealy FSM. Often, in a Moore FSM, the specific output pattern defines what it means to be in the current state. In the following videos we take a simplistic system where we wish to detect if a input stream has a odd number of 1s so far.  It does not lend itself to an easy implementation because  we do not have a notion of how long a bit has to persist for it to be inferred as the same bit as opposed to a new bit. It serves though as a simple example.  The later examples are more rigorously specified and therefore lend themselves to proper implementations.

Video 4.4.2. Odd 1's Detector FSM - Linked Data Structure

Video 4.4.3. Odd 1's Detector FSM - FSM Controller

Example 4.4.1. Design a traffic light controller for the intersection of two equally busy one-way streets. The goal is to maximize traffic flow, minimize waiting time at a red light, and avoid accidents.

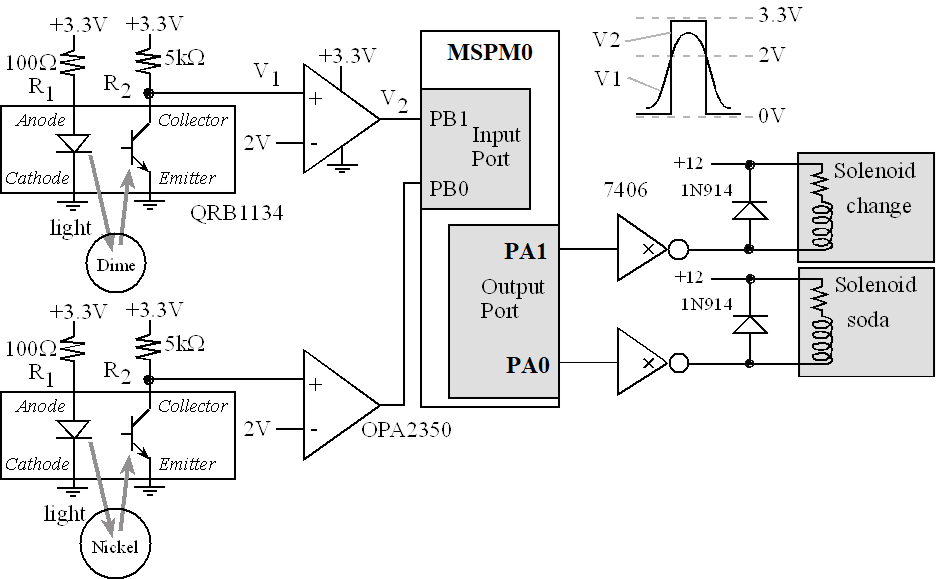
Solution: The intersection has two one-ways roads with the same amount of traffic: North and East, as shown in Figure 4.4.2. Controlling traffic is a good example because we all know what is supposed to happen at the intersection of two busy one-way streets. We begin the design defining what constitutes a state. In this system, a state describes which road has authority to cross the intersection. The basic idea, of course, is to prevent southbound cars to enter the intersection at the same time as westbound cars. In this system, the light pattern defines which road has right of way over the other. Since an output pattern to the lights is necessary to remain in a state, we will solve this system with a Moore FSM. It will have two inputs (car sensors on North and East roads) and six outputs (one for each light in the traffic signal.)  The six traffic lights are interfaced to Port B bits 5–0, and the two sensors are connected to Port B bits 7–6,

 

PB7=0, PB6=0 means no cars exist on either road

PB7=0, PB6=1 means there are cars on the East road

PB7=1, PB6=0 means there are cars on the North road

PB7=1, PB6=1 means there are cars on both roads

 

The next step in designing the FSM is to create some states. Again, the Moore implementation was chosen because the output pattern (which lights are on) defines which state we are in. Each state is given a symbolic name:

 

goN,                 PB5-0 = 100001 makes it green on North and red on East

waitN,            PB5-0 = 100010 makes it yellow on North and red on East

goE,                 PB5-0 = 001100 makes it red on North and green on East

waitE,            PB5-0 = 010100 makes it red on North and yellow on East

 

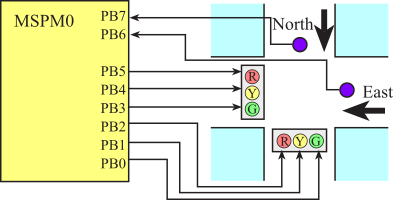
Figure 4.4.2. Traffic light interface with two sensors and 6 lights.

 

The output pattern for each state is drawn inside the state circle. The time to wait for each state is also included. How the machine operates will be dictated by the input-dependent state transitions. We create decision rules defining what to do for each possible input and for each state. For this design we can list heuristics describing how the traffic light is to operate:

 

If no cars are coming, stay in a green state, but which one doesn’t matter.

To change from green to red, implement a yellow light of exactly 5 seconds.

Green lights will last at least 30 seconds.

If cars are only coming in one direction, move to and stay green in that direction.

If cars are coming in both directions, cycle through all four states.

 

Before we draw the state graph, we need to decide on the sequence of operations.

 

            1. Initialize timer and direction registers

            2. Specify initial state

            3. Perform FSM controller

                        a) Output to traffic lights, which depends on the state

                        b) Delay, which depends on the state

                        c) Input from sensors

                        d) Change states, which depends on the state and the input

 

We implement the heuristics by defining the state transitions, as illustrated in Figure 4.4.3. Instead of using a graph to define the finite state machine, we could have used a table, as shown in Table 5.2.

 

Figure 4.4.3. Graphical form of a Moore FSM that implements a traffic light.

 

 

A state transition table has exactly the same information as the state transition graph, but in tabular form. The first column specifies the state number, which we will number  sequentially from 0. Each state has a descriptive name. The "Lights" column defines the output patterns for six traffic lights. The "Time" column is the time to wait with this output. The last four columns will be the next states for each possible input pattern.

Num	Name	Lights	Time	In=0	In=1	In=2	In=3
0	goN	100001	30	goN	waitN	goN	waitN
1	waitN	100010	5	goE	goE	goE	goE
2	goE	001100	30	goE	goE	waitE	waitE
3	waitE	010100	5	goN	goN	goN	goN

Table 4.4.1. Tabular form of a Moore FSM that implements a traffic light.

 

 

The next step is to map the FSM graph onto a data structure that can be stored in ROM. Program 4.4.1 uses an array of structures, where each state is an element of the array, and state transitions are defined as indices to other nodes. The four Next parameters define the input-dependent state transitions. The wait times are defined in the software as decimal numbers with units of 10ms, giving a range of 10 ms to about 10 minutes. Using good labels makes the program easier to understand, in other words goN is more descriptive than 0.

The main program begins by specifying the Port B bits 7 and 6 to be inputs and Port B bits 5–0 to be outputs. The initial state is defined as goN. The main loop of our controller first outputs the desired light pattern to the six LEDs, waits for the specified amount of time, reads the sensor inputs from Port B bits 7 and 6, and then switches to the next state depending on the input data. The timer functions were presented earlier as Program 5.2. The function SysTick_Wait10ms will wait 10ms times the parameter. We will implement friendly access to Port B.

Video 4.4.4. Traffic Light Demo

Video 4.4.5. Traffic Light FSM***needs recording***

 

// Linked data structure
struct State {
  uint32_t Out;
  uint32_t Time;
  const struct State *Next[4];};
typedef const struct State State_t;
#define goN &FSM[0]
#define waitN &FSM[1]
#define goE &FSM[2]
#define waitE &FSM[3]
State_t FSM[4]={
  {0x21,3000,{goN,waitN,goN,waitN}},
  {0x22, 500,{goE,goE,goE,goE}},
  {0x0C,3000,{goE,goE,waitE,waitE}},
  {0x14, 500,{goN,goN,goN,goN}}};
State_t *Pt; // state pointer
int main(void){ uint32_t Input;
  Clock_Init80MHz(0);
  SysTick_Init();
  Traffic_Init();
  Pt = goN;
  while(1){
    GPIOB->DOUT31_0 = (GPIOB->DOUT31_0&(~0x3F))|Pt->Out;
    SysTick_Wait10ms(Pt->Time);
    Input = (GPIOB->DIN31_0&0xC0)>>6;
    Pt = Pt->Next[Input];
  }
}

}

Program 4.4.1. Linked data structure implementation of the traffic light controller.

 

In order to make it easier to understand, which will simplify verification and modification, we have made a 1-to-1 correspondence between the state graph in Figure 4.4.3 and the FSM[4] data structure in Program 4.4.1. Notice also how this implementation separates the civil engineering policies (the data structure specifies what the machine does), from the computer engineering mechanisms (the executing software specifies how it is done.)  Once we have proven the executing software to be operational, we can modify the policies and be confident that the mechanisms will still work. When an accident occurs, we can blame the civil engineer that designed the state graph.

On microcontrollers that have flash, we can place the FSM data structure in flash. This allows us to make minor modifications to the finite state machine (add/delete states, change input/output values) by changing the data structure. In this way small modifications/upgrades/options to the finite state machine can be made by reprogramming the flash reusing the hardware external to the microcontroller.

The FSM approach makes it easy to change. To change the wait time for a state, we simply change the value in the data structure. To add more states (e.g., put a red/red state after each yellow state, which will reduce accidents caused by bad drivers running the yellow light), we simply increase the size of the fsm[] structure and define the Out, Time, and Next fields for these new states.

To add more output signals (e.g., walk and left turn lights), we simply increase the precision of the Out field. To add two more input lines (e.g., wait button, left turn car sensor), we increase the size of the next field to Next[16]. Because now there are four input lines, there are 16 possible combinations, where each input possibility requires a Next value specifying where to go if this combination occurs. In this simple scheme, the size of the Next[] field will be 2 raised to the power of the number of input signals.

Checkpoint 4.4.1: Why is it good to use labels for the states? E.g., why is goN is better than &FSM[0]?

Checkpoint 4.4.2: Is the output to Port B friendly? If so, why is it friendly? If not, how would you change it to be friendly?

Observation: In order to make the FSM respond quicker, we could implement a time delay function that returns immediately if an alarm condition occurs. If no alarm exists, it waits the specified delay.

Example 4.4.2. Design vending machine with two outputs (soda, change) and two inputs (dime, nickel).

Solution:  This vending machine example illustrates additional flexibility that we can build into our FSM implementations. In particular, rather than simple digital inputs, we will create an input function that returns the current values of the inputs. Similarly, rather than simple digital outputs, we will implement general functions for each state. We could have solved this particular vending machine using the approach in the previous example, but this approach provides an alternative mechanism when the input and/or output operations become complex. Our simple vending machine has two coin sensors, one for dimes and one for nickels, see Figure 4.4.4. When a coin falls through a slot in the front of the machine, light from the QEB1134 sensor reflects off the coin and is recognized back at the sensor. An op amp (OPA2350) creates a digital high at the Port B input whenever a coin is reflecting light. So as the coin passes the sensor, a pulse (V2) is created. The two coin sensors will be inputs to the FSM. If the digital input is high (1), this means there is a coin currently falling through the slot. When a coin is inserted into the machine, the sensor goes high, then low. Because of the nature of vending machines we will assume there cannot be both a nickel and a dime at the same time. This means the FSM input can be 0, 1, or 2. To implement the soda and change dispensers, we will interface two solenoids to Port A. The coil current of the solenoids is less than 40 mA, so we can use the 7406 open collector driver. If the software makes PA0 high, waits 10ms, then makes PA0 low, one soda will be dispensed. If the software makes PA1 high, waits 10ms, then makes PA1 low, one nickel will be returned.

 

Figure 4.4.4. A vending machine interfaced to a microcontroller.

We need to decide on the sequence of operations before we draw the state graph.

      1) Initialize timer and directions registers

      2) Specify initial state

      3) Perform FSM controller

                    a) Call an output function, which depends on the state

                    b) Delay, which depends on the state

                    c) Call an input function to get the status of the coin sensors

                    d) Change states, which depends on the state and the input.

 

Figure 4.4.5 shows the Moore FSM that implements the vending machine. A soda costs 15 cents, and the machine accepts nickels (5 cents) and dimes (10 cents). We have an input sensor to detect nickels (bit 0) and an input sensor to detect dimes (bit 1.) We choose the wait time in each state to be 20ms, which smaller than the time it takes the coin to pass by the sensor. Waiting in each state will debounce the sensor, preventing multiple counting of a single event. Notice that we wait in all states, because the sensor may bounce both on touch and release. Each state also has a function to execute.  The function Soda will trigger the Port A output so that a soda is dispensed. Similarly, the function Change will trigger the Port A output so that a nickel is returned. The M states refer to the amount of collected money. When we are in a W state, we have collected that much money, but we’re still waiting for the last coin to pass the sensor. For example, we start with no money in state M0. If we insert a dime, the input will go 10₂, and our state machine will jump to state W10. We will stay in state W10 until the dime passes by the coin sensor. In particular when the input goes to 00, then we go to state M10. If we insert a second dime, the input will go 10₂, and our state machine will jump to state W20. Again, we will stay in state W20 until this dime passes. When the input goes to 00, then we go to state M20. Now we call the function change and jump to state M15. Lastly, we call the function Soda and jump back to state M0.

Figure 4.4.5. This Moore FSM implements a vending machine.

 

Since this is a layered system, we will begin by designing the low-level input/output functions that handle the operation of the sensors and solenoid, see Program 4.4.2. The initialization specifies Port B bits 1 and 0 to be input and the Port A bits 1 and 0 to be outputs. The PLL and SysTick are also initialized.

 

#define T10ms 800000
#define T20ms 1600000
void FSM_Init(void){
  Clock_Init80MHz(0);
  LaunchPad_Init(); // reset, activate Port A Port B
  SysTick_Init();
  IOMUX->SECCFG.PINCM[PB0INDEX] = 0x00040081; // GPIO input
  IOMUX->SECCFG.PINCM[PB1INDEX] = 0x00040081; // GPIO input
  IOMUX->SECCFG.PINCM[PA0INDEX] = 0x00000081; // GPIO output
  IOMUX->SECCFG.PINCM[PA1INDEX] = 0x00000081; // GPIO output
  GPIOA->DOE31_0 |= 0x03;     // enable output PA1 PA0
  GPIOA->DOUT31_0 &= ~0x03;   // deactivate
}
uint32_t Coin_Input(void){
  return GPIOB->DIN31_0&0x03; // PB1,0 can be 0, 1, or 2
}
void Solenoid_None(void){
};
void Solenoid_Soda(void){
  GPIOA->DOUT31_0 |= 0x01;  // activate solenoid
  SysTick_Wait(T10ms);      // 10 msec, dispenses a delicious soda
  GPIOA->DOUT31_0 &= ~0x01; // deactivate
}
void Solenoid_Change(void){
  GPIOA->DOUT31_0 |= 0x02;  // activate solenoid
  SysTick_Wait(T10ms);      // 10 msec, return 5 cents
  GPIOA->DOUT31_0 &= ~0x02; // deactivate
}

Program 4.4.2. Low-level input/output functions for the vending machine.

The initial state is defined as M0. Our controller software first calls the function for this state, waits for the specified amount of time, reads the sensor inputs from Port B, then switches to the next state depending on the input data. Notice again the 1-to-1 correspondence between the state graph in Figure 4.4.5 and the data structure in Program 4.4.2.

 

struct State {

  void (*CmdPt)(void); // output function

  uint32_t Time;       // wait time, 12.5ns units

  uint32_t Next[3];};

typedef const struct State State_t;

#define M0  0

#define W5  1

#define M5  2

#define W10 3

#define M10 4

#define W15 5

#define M15 6

#define W20 7

#define M20 8

State_t FSM[9]={

  {&Solenoid_None,  T20ms,{M0,W5,W10}},      // M0, no money

  {&Solenoid_None,  T20ms,{M5,W5,W5}},       // W5, seeing a nickel

  {&Solenoid_None,  T20ms,{M5,W10,W15}},     // M5, have 5 cents

  {&Solenoid_None,  T20ms,{M10,W10,W10}},    // W10, seeing a dime

  {&Solenoid_None,  T20ms,{M10,W15,W20}},    // M10, have 10 cents

  {&Solenoid_None,  T20ms,{M15,W15,W15}},    // W15, seeing something

  {&Solenoid_Soda,  T20ms,{M0,M0,M0}},       // M15, have 15 cents

  {&Solenoid_None,  T20ms,{M20,W20,W20}},    // W20, seeing dime

  {&Solenoid_Change,T20ms,{M15,M15,M15}}};   // M20, have 20 cents

uint32_t S; // index into current state    

uint32_t Input;

int main(void){ 

  FSM_Init();

  S = M0;       // Initial State

  while(1){

    (FSM[S].CmdPt)();           // call output function

    SysTick_Wait(FSM[S].Time);  // wait

    Input = Coin_Input();       // input can be 0,1,2

    S = FSM[S].Next[Input];     // next

  }

}

Program 5.6. Vending machine controller.

Interactive Tool 4.4.1

A simulation of a Vending machine dispensing soda with the corresponding FSM state changes

 

Quiz 4.4

Grade Quiz

 

4.5. Stepper motors (optional for ECE319K)

A motor can be evaluated in terms of its maximum speed (RPM), its torque (N-m), and the efficiency in which it translates electrical power into mechanical power. Sometimes however, we wish to use a motor to control the rotational position (θ=motor shaft angle) rather than to control the rotational speed (ω=dθ/dt). Stepper motors are used in applications where precise positioning is more important than high RPM, high torque, or high efficiency. Stepper motors are very popular for microcontroller-based embedded systems because of their inherent digital interface. This next video shows a stepper motor controlled by a FSM. The first button makes it spin one way, the second button makes it spin the other way, and the third button makes it step just once. If both the first two buttons are pressed it wiggles back and forth.

Video 4.5.1. A Simple Stepper Motor***needs recording***

 

Larger motors provide more torque, but require more current. It is easy for a computer to control both the position and velocity of a stepper motor in an open-loop fashion. Although the cost of a stepper motor is typically higher than an equivalent DC permanent magnetic field motor, the overall system cost is reduced because stepper motors may not require feedback sensors. They are used in printers to move paper and print heads, tapes/disks to position read/write heads, and high-precision robots.

A bipolar stepper motor has two coils on the stator (the frame of the motor), labeled A and B in Figure 4.5.1. Typically, there is always current flowing through both coils. When current flows through both coils, the motor does not spin (it remains locked at that shaft angle). Stepper motors are rated in their holding torque, which is their ability to hold stationary against a rotational force (torque) when current is constantly flowing through both coils. To move a bipolar stepper, we reverse the direction of current through one (not both) of the coils, see Figure 4.5.1. To move it again we reverse the direction of current in the other coil. Remember, current is always flowing through both coils. Let the direction of the current be signified by up and down arrows in Figure 4.5.1. To make the current go up, the microcontroller outputs a binary 01 to the interface. To make the current go down, it outputs a binary 10. Since there are 2 coils, four outputs will be required (e.g., 0101₂ means up/up). To spin the motor, we output the sequence 0101₂, 0110₂, 1010₂, 1001₂… over and over. Each output causes the motor to rotate a fixed angle. To rotate the other direction, we reverse the sequence (0101₂, 1001₂, 1010₂, 0110₂…). 

Figure 4.5.1. A bipolar stepper has 2 coils, but a unipolar stepper divides those two coils into four parts.

There is a North and a South permanent magnet on the rotor (the part that spins). The amount of rotation caused by each current reversal is a fixed angle depending on the number of teeth on the permanent magnets. For example, the rotor in Figure 4.5.2 is drawn with one North tooth and one South tooth. If there are n teeth on the South magnet (also n teeth on the North magnet), then the stepper will move at 90/n degrees. This means there will be 4n steps per rotation. Because moving the motor involves accelerating a mass (rotational inertia) against a load friction, after we output a value, we must wait an amount of time before we can output again. If we output too fast, the motor does not have time to respond. The speed of the motor is related to the number of steps per rotation and the time in between outputs. For information on stepper motors see the data sheets
StepperBasic.pdf
StepperDriveBasic.pdf
StepperSelection.pdf
Stepper.pdf
Stepper_ST.pdf

 

Figure 4.5.2. To rotate this stepper by 18^o, the interface flips the direction of one of the currents.

Interactive Tool 4.5.1

Click 'CW' or 'CCW' to step the motor clockwise and counterclockwise, respectively. Observe how different microcontroller outputs to the motor coils produce different responses from the motor. Assume that an output value of '1' to a motor coil will cause current to flow in that motor, resulting in a 'N' oriented magnetic field at that coil.

Checkpoint 4.5.1: What is the output sequence that produces one complete counterclockwise rotation in the motor? 

Checkpoint 4.5.2: What is the output sequence that results in one complete clockwise rotation in the motor?

Checkpoint 4.5.3: Identify two sets of output values in the sequence that will never occur one after the other.

The unipolar stepper motor provides for bi-directional currents by using a center tap, dividing each coil into two parts. In particular, coil A is split into coil A and A’, and coil B is split into coil B and B’. The center tap is connected to the +V power source and the four ends of the coils can be controlled with open collector drivers. Because only half of the electro-magnets are energized at one time, a unipolar stepper has less torque than an equivalent-sized bipolar stepper. However, unipolar steppers are easier to interface. For more information on interfacing stepper motors see Volume 2, Embedded Systems: Real-Time Interfacing to ARM® Cortex™-M Microcontrollers.

Figure 4.5.3 shows a circular linked graph containing the output commands to control a stepper motor. This simple FSM has no inputs, four output bits and four states. There is one state for each output pattern in the usual stepper sequence 5,6,10,9... The circular FSM is used to spin the motor is a clockwise direction.

Figure 4.5.3. This stepper motor FSM has four states. The 4-bit outputs are given in binary.

Example 4.5.1. Design an autonomous robot using FSMs and stepper motors. Make the robot avoid walls.

Video 4.5.2. Robot Car - Problem Statement and STG ***needs recording***

Solution: We choose a stepper motor according to the speed and torque requirements of the system. A stepper with 200 steps/rotation will provide a very smooth rotation while it spins. Just like the DC motor, we need an interface that can handle the currents required by the coils. We can use a L293 to interface either unipolar or bipolar steppers that require less than 1 A per coil. In general, the output current of a driver must be large enough to energize the stepper coils. We control the interface using an output port of the microcontroller, as shown in Figure 4.5.4. Motors require interface circuits, like the L293, because of the large currents required for the motor. Furthermore, most motors will require more current than the USB or LaunchPad can supply. In this system the motors are powered directly from an 8.4V battery. Motor current flows from the battery to the L293, out 1Y, across the coil of the stepper motor, into the 2Y-pin of the L293, and finally back to the battery. Notice the motor currents do not flow across the LaunchPad or in/out the USB. The circuit shows the interface of two bipolar steppers, but the unipolar stepper interface is similar except there would be a direct connection of +8.4V to the motor (see Figure 4.5.4). The front of the robot has two bumper switches. The 7805 regulator allows the LaunchPad to be powered from the battery.

 

Figure 4.5.4. Two bipolar stepper motors interfaced to a microcontroller allow the robot to move. The dark lines carry large currents. Bipolar stepper motors have 4 wires.

 

Figure 4.5.5. Two unipolar stepper motors interfaced to a microcontroller allow the robot to move. The dark lines carry large currents. Unipolar stepper motors have 5 or 6 wires.

To make the robot move forward (states 0,1,2,3) we spin both motors. To satisfy Isaac Asimov’s first law of robotics “A robot may not injure a human being or, through inaction, allow a human being to come to harm”, we will add two bumper switches in the front that will turn the robot if it detects an object in its path. To make the robot move backward (states S3, S2, S1, S0), we step both motors the other direction. We turn right by stepping the right motor back and the left motor forward (states S0, S7, S8, S9). We turn left by stepping the left motor back and the right motor forward (states S0, S4, S5, S6). Figure 4.5.6 shows the FSM to control this simple robot. This FSM has two inputs, so each state has four next states. Notice the 1-to-1 correspondence between the state graph in Figure 5.15 and the FSM[10] data structure in Program 4.5.1.

Figure 4.5.6. If the bumpers are not active (00) the both motor spin at 15 RPM, if both bumpers are active the robot backs up, if just the right bumper is active it turns left, and if just the left bumper is active, it turns right.

 

The main program, Program 4.5.1, begins by initializing all of Ports B to be an output and PA1,PA0 to be an input. There are ten states in this robot. If the bumper switch activates, it attempts to turn away from the object. Every 20 ms the program outputs a new stepper commands to both motors. The function SysTick_Wait10ms()generates an appropriate delay between outputs to the stepper. For a 200 step/rotation stepper, if we wait 20 ms between outputs, there will be 50 outputs/sec, or 3000 outputs/min, causing the stepper motor to spin at 15 RPM. When calculating speed, it is important to keep track of the units.

 

Speed = (1 rotation/200 steps)*(1000ms/s)*(60sec/min)*(1step/20ms) = 15 RPM

Video 4.5.3. Robot Car - Software***needs recording***

Video 4.5.4. Robot Car - Demo ***needs recording***

 

 

// represents a State of the FSM

struct State{

  uint8_t out;     // PB7-4 to right motor, PB3-0 to left         

  uint16_t wait;   // in 10ms units      

  uint8_t next[4]; // input 0x00 means ok,

                   //       0x01 means right side bumped something,

                   //       0x02 means left side bumped something,

                   //       0x03 means head-on collision (both sides bumped something)

};

typedef const struct State State_t;

State_t Fsm[10] = {

  {0x55, 2, {1, 4, 7, 3} }, // S0) initial state and state where bumpers are checked

  {0x66, 2, {2, 2, 2, 0} }, // S1) both forward [1]

  {0xAA, 2, {3, 3, 3, 1} }, // S2) both forward [2]

  {0x99, 2, {0, 0, 0, 2} }, // S3) both forward [3]

  {0x69, 5, {5, 5, 5, 5} }, // S4) left forward; right reverse [1] turn left

  {0xAA, 5, {6, 6, 6, 6} }, // S5) left forward; right reverse [2] turn left

  {0x96, 5, {0, 0, 0, 0} }, // S6) left forward; right reverse [3] turn left

  {0x96, 5, {8, 8, 8, 8} }, // S7) left reverse; right forward [1] turn right

  {0xAA, 5, {9, 9, 9, 9} }, // S8) left reverse; right forward [2] turn right

  {0x69, 5, {0, 0, 0, 0} }  // S9) left reverse; right forward [3] turn right

};

 

void Robot_Init(void){
  IOMUX->SECCFG.PINCM[PA0INDEX] = 0x00040081; // GPIO input
  IOMUX->SECCFG.PINCM[PA1INDEX] = 0x00040081; // GPIO input
  IOMUX->SECCFG.PINCM[PB0INDEX] = 0x00000081; // GPIO output
  IOMUX->SECCFG.PINCM[PB1INDEX] = 0x00000081; // GPIO output
  IOMUX->SECCFG.PINCM[PB2INDEX] = 0x00000081; // GPIO output
  IOMUX->SECCFG.PINCM[PB3INDEX] = 0x00000081; // GPIO output
  IOMUX->SECCFG.PINCM[PB4INDEX] = 0x00000081; // GPIO output
  IOMUX->SECCFG.PINCM[PB5INDEX] = 0x00000081; // GPIO output
  IOMUX->SECCFG.PINCM[PB6INDEX] = 0x00000081; // GPIO output
  IOMUX->SECCFG.PINCM[PB7INDEX] = 0x00000081; // GPIO output
  GPIOB->DOE31_0 |= 0xFF;     // enable output PB7-PB0
}

 

uint8_t cState;      // current State (0 to 9)

int main(void){

  uint8_t input;

  Clock_Init80MHz(0);                     

  SysTick_Init();                 

  LaunchPad_Init();                // reset, activate Port A Port B

  Robot_Init();                    // initialize motor outputs on Port B, initialize sensor inputs on Port A

  cState = 0;                      // initial state = 0

  while(1){

    // output based on current state

    GPIOB->DOUT31_0 = (GPIOB->DOUT31_0 & ~0xFF)| Fsm[cState].out; // step motor

    // wait for time according to state

    SysTick_Wait10ms(Fsm[cState].wait);

    // get input    

    input = GPIOA->DIN31_0&0x03; // Input 0,1,2,3

    // change the state based on input and current state

    cState = Fsm[cState].next[input];

  }

}

Program 4.5.1. Stepper motor controller.

 

To illustrate how easy it is to make changes to this implementation, let’s consider these three modifications. To make it spin in the other direction, we simply change pointers to sequence in the other direction. We could also add additional input pins and make it perform other commands. To make it travel at a different speed, we change the wait time.

Checkpoint 4.5.4: If the stepper motor were to have 36 steps per rotation, how fast would the two motors spin using Program 4.5.1? 

Checkpoint 4.5.5: What would you change in Program 4.5.1 to make the motor spin at 30 RPM? 

Checkpoint 4.5.6: Does the robot in the previous example satisfy Asimov’s second law of robotics? 

Performance tip: Use a DC motor for applications requiring high torque or high speed, and use a stepper motor for applications requiring accurate positioning at low speed.

Performance tip: To get high torque at low speed, use a geared DC motor (the motor spins at high speed, but the shaft spins slowly).

Go to Chapter 5: Interrupts, Digital to Analog Conversion (DAC), and Sound Generation

  This material was created to teach ECE319K at the University of Texas at Austin

Reprinted with approval from Introduction to Embedded Systems Using the MSPM0+, ISBN: 979-8852536594

 
Embedded Systems - Shape the World by Jonathan Valvano and Ramesh Yerraballi is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
Based on a work at http://users.ece.utexas.edu/~valvano/mspm0/

.