Chapter
7: Analog to Digital Conversion, Data Acquisition, and Control
Jonathan
Valvano and Ramesh Yerraballi
Throughout this course we have seen that an embedded system uses its input/output devices to interact with the external world. In this chapter we will focus on input devices that we use to gather information about the world. More specifically, we present a technique for the system to measure analog inputs using an analog to digital converter (ADC). We will use periodic interrupts to sample the ADC at a fixed rate. We define the rate at which we sample as the sampling rate, and use the symbol fs. We will then combine sensors, the ADC, software, PWM output and motor interfaces to implement intelligent control on our robot car.
Table of Contents:
- 7.1.
Data Acquisition and Control Systems
- 7.2. The Analog to Digital Converter
- 7.3.
Details of the ADC on the MSPM0
- 7.4.
Nyquist Theorem
- 7.5.
Central Limit Theorem
- 7.6.
C++ on the MSPM0, ECE319H only
- 7.7.
Periodic Interrupt using Timers
- 7.8.
ECE319K Lab 7 videos
- 7.9.
Robot Car Controller, ECE319K/ECE319H students can skip section 7.9
Return to book table of contents
Video 7.0. Introduction to Digitization
7.1. Data Acquisition and Control Systems
Video 7.1.1. Digitization Concepts.
The measurand is a real world signal of interest like sound, distance, temperature, force, mass, pressure, flow, light and acceleration. Figure 7.1.1 shows the data flow graph for a data acquisition system or control system. x(t) is the time-varying signal we are attempting to measure. The control system uses an actuator to drive a measurand in the real world to a desired value while the data acquisition system has no actuator because it simply measures the measurand in a nonintrusive manner. Consider an entire system that collects data, not just the ADC. The following four limitations exist when sampling data.
- Amplitude resolution
- Amplitude range
- Time quantization
- Time interval
Amplitude resolution is the smallest change in input signal that can be distinguished. For example, we might specify the resolution as dX. Amplitude range is defined as the smallest to largest input value that can be measured. For example, we might specify the range as Xmin to Xmax. Amplitude precision is defined as the number of distinct values from which the measurement is selected. The units of precision are given in alternative or bits. If a system has 12-bit precision, there are 2^12 or 4096 distinct alternatives. For example if we use a slide pot to measure distance, the range of that pot might be 0 to 2cm. If there is no electrical noise and we use a 12-bit ADC, then the theoretical resolution is 2cm/4095, or about 0.0005 cm. In most systems, the resolution of the measurement is determined by noise and not the number of bits in the ADC. Time quantization is the time difference between one sample and the next. Time interval is the smallest to largest time during which we collect samples. If we use a 10-Hz SysTick interrupt to sample the ADC and calculate distance, the sampling rate, fs, is 10 Hz, and the time quantization is 1/fs=0.1 sec. If we use a memory buffer with 500 elements, then the time interval is 0 to 50 sec.
: Assume Xmin, Xmax, and dX are all given in the same units. Give a formula that relates the precision in bits as a function of Xmin, Xmax and dX.
: Assume the precision is n in bits, and Xmin, Xmax, and dX are all given in the same units. Give a formula that relates the resolution, dX as a function of Xmin, Xmax and n.
: Assume you have a 12-bit ADC and store data into an array of type uint16_t. Let fs be the sampling rate in Hz, and T be the total time interval required to collect samples in sec. Give a formula that relates needed memory in bytes as a function of fs and T.
: Assume you have an 8-bit ADC. Let the sampling rate be 100 Hz. Assume you allocate 20,000 out of the available 32,768 bytes of RAM to store the data. What is the corresponding time interval? I.e., how many seconds of data can you record?
: Assume you have a 4-bit DAC used to play sound. Let the sampling rate be 11 kHz. You can pack two DAC samples into one byte. Assume you allocate 128 kibibytes out of the available 256 kibibytes of ROM to store the data. What is the corresponding time interval? I.e., how many seconds of sound can you play?
Observation: Amplitude resolution is range divided by precision in alternatives.
Observation: Frequency resolution is the sampling rate divided the number of samples, which is also equal to 1 divided by the time interval.
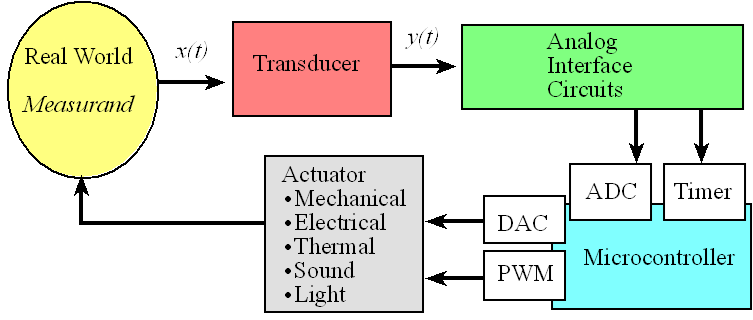
Figure 7.1.1. Signal paths a data acquisition system.
The input or measurand is x. A transducer converts x into y. The analog circuit converts the transducer output into a signal that the microcontroller can process. In this chapter, our circuits will connect to the analog to digital converter (ADC) on the microcontroller. A wide variety of inexpensive sensors can be seen at https://www.sparkfun.com/categories/23 Examples include
· Sound Microphone
· Pressure, mass, force Strain gauge, force sensitive resistor
· Temperature Thermistor, thermocouple, integrated circuits
· Distance Ultrasound, lasers, infrared light
· Flow Doppler ultrasound, flow probe
· Acceleration Accelerometer
· Light Camera
· Biopotentials Silver-Silver Chloride electrode
A linear transducer is an input/output function fits a straight line. In other words, the input/output response fits a linear equation:
y = m*x+b
where m and b are constants. Software will have an easy time with a linear transducer. Figure 7.1.2 shows the linear potentiometer, PTA2043-2015CPB103, where R1+R2 is fixed at 10kΩ, and R2 varies with the position of the movable arm of the potentiometer. A potentiometer has three pins, labeled Pin 1 2 3 in the figure. Notice also that R1=10kΩ-R2, so both R1 and R2 change as the arm is moved.


Figure 7.1.2. The linear potentiometer can be used to measure distance.
The PTA2043-2015CPB103 has a transfer function as shown in Figure 7.1.3, where the input x is distance in cm, and the output y=R2 is the resistance in kΩ.
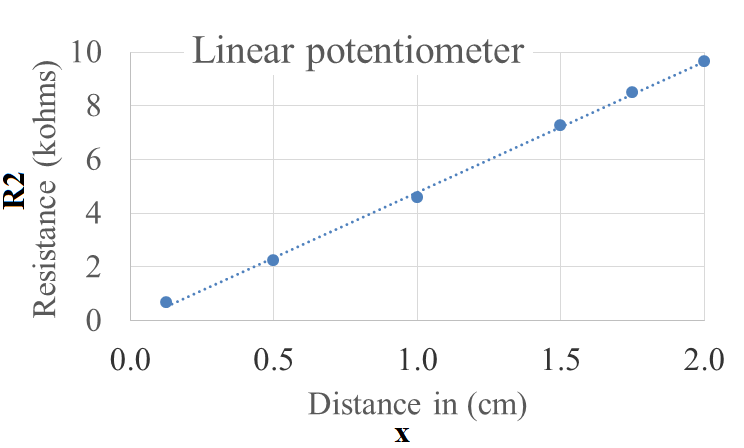
Figure 7.1.3. The linear potentiometer distance sensor exhibits linear behavior.
Figure 7.1.4 shows a simple circuit to convert resistance to voltage. The ADC will convert voltage to an integer, and simple software will convert an integer to distance. Notice a distance of 0 cm will map to 0.0V on pin PB18, and a distance of 2 cm will map to 3.3V. Because the current through the sensor is fixed at 3.3V/10kΩ, the voltage at PB18 will be a linear function of distance.
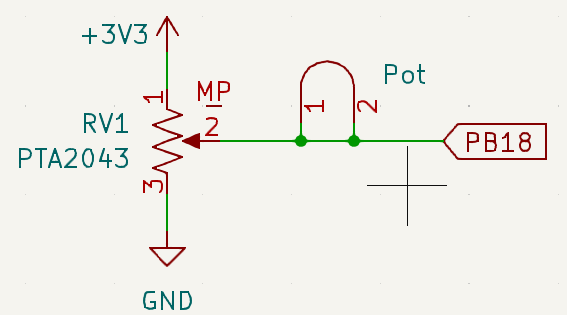
Figure 7.1.4. Circuit interfacing the sensor to the microcontroller.
: Consider the linear potentiometer in Figure 7.1.3. Let x be the distance in cm and let y=R2 be the resistance in kohm. Give an appropriate transfer function showing y as a function of x.
: Consider the interface in Figure 7.1.4. Let x be the distance in cm and let V be the voltage on pin PB18 in volts. Give an appropriate transfer function showing V as a function of x.
A nonmonotonic transducer is an input/output function that does not have a mathematical inverse. For example, if two or more input values yield the same output value, then the transducer is nonmonotonic. Software will have a difficult time correcting a nonmonotonic transducer. For example, the Sharp GP2Y0A21YK IR distance sensor has a transfer function as shown in Figure 7.1.5. If you read a transducer voltage of 2 V, you cannot tell if the object is 3 cm away or 12 cm away. However, if we assume the distance is always greater than 10cm, then this transducer can be used.

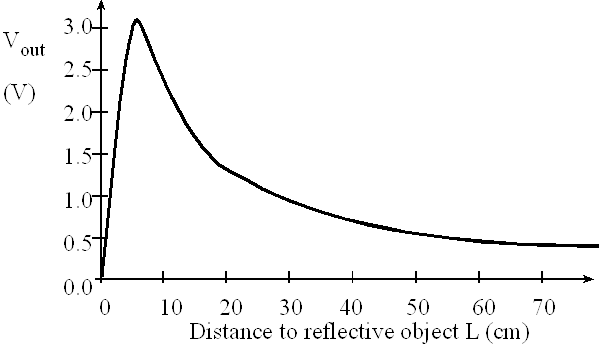
Figure 7.1.5. The Sharp IR distance sensor exhibits nonmonotonic behavior.
Quiz 7.1
7.2. The Analog to Digital Converter
An analog to digital converter (ADC) converts an analog signal into digital form, shown in Figure 7.2.1. An embedded system uses the ADC to collect information about the external world (data acquisition system.) The input signal is usually an analog voltage, and the output is a binary number. The ADC precision is the number of distinguishable ADC inputs (e.g., 4096 alternatives, 12 bits). The ADC range is the maximum and minimum ADC input (e.g., 0 to +3.3V). The ADC resolution is the smallest distinguishable change in input (e.g., 3.3V/4095, which is about 0.81 mV). The resolution is the change in input that causes the digital output to change by 1.
Range(volts) = Precision(alternatives) • Resolution(volts)
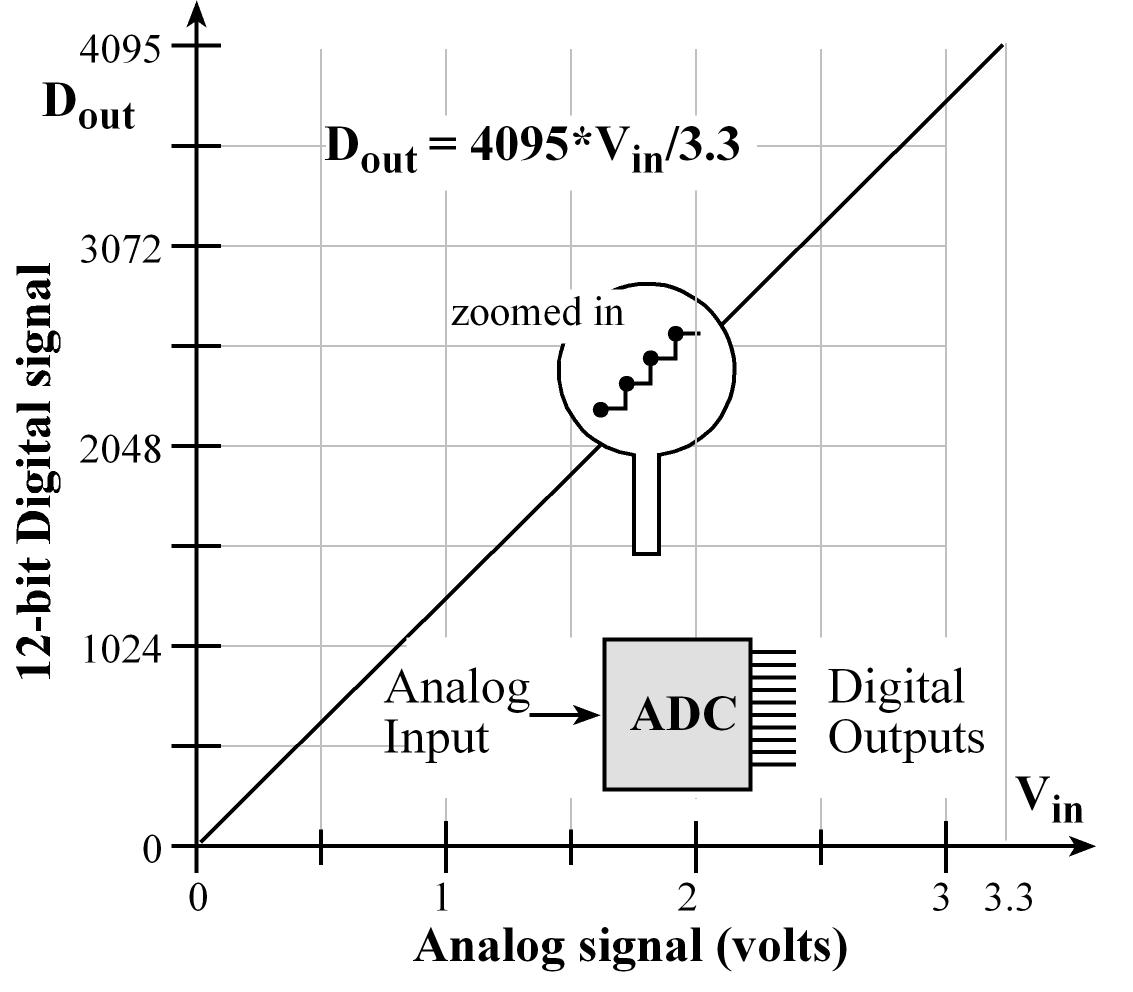
Figure 7.2.1. A 12-bit ADC converts 0 to 3.3V on its input into a digital number from 0 to 4095.
This tool allows you to
see the progression of a simple data acquisition system. Distance
is the parameter to be measured, and it is defined as the distance in cm of
the handle to the left side of the pot. The potentiometer has
three terminals, as shown previously in Figure 7.1.4, such that R1+R2 always
sums to 10kΩ, and the resistance R2 varies from 0 to 10kΩ, and
linearly depends on Distance.
The Voltage at the ADC converter linearly depends on R2.
The Digital value of the ADC conversition linearly depends on the
analog input.
The software will convert the Digital value into the Integer part
of a decimal fixed-point number, with a resolution of 0.01cm.
Integer = (2000*Digital)>>12;
Exercise 1: Drag the handle to the left and right to see the distance varies from 0 to 2cm.
Exercise 2: Drag the handle to the left and right to see R2= 10000Ω*Distance/2cm.
Exercise 3: Drag the handle to the left and right to see Voltage= 3.3V*R2/10kΩ.
Exercise 4: Drag the handle to the left and right to see Digital= 4095*Voltage/3.3V.
Exercise 5: Drag the handle to the left and right to see Integer in software accurately represents the original Distance.
The most pervasive method for ADC conversion is the successive approximation technique, as illustrated in Figure 7.2.2. A 12-bit successive approximation ADC is clocked 12 times. At each clock another bit is determined, starting with the most significant bit. For each clock, the successive approximation hardware issues a new "guess" on Vdac by setting the bit under test to a "1". If Vdac is now higher than the unknown input, Vin, then the bit under test is cleared. If Vdac is less than Vin, then the bit under test is remains 1. In this description, bit is an unsigned integer that specifies the bit under test. For a 12-bit ADC, bit goes 2048, 1024, 512, 256,...,1. Dout is the ADC digital output, and Z is the binary input that is true if Vdac is greater than Vin.

Figure 7.2.2. A 12-bit successive approximation ADC.
Video 7.2.1. Successive Approximation
This tool allows you to
go through the motions of a ADC sample capture using successive
approximation. It is a game to demonstrate successive approximation.
There is a secret number between 0 to 63 (6-bit ADC) that the computer
has selected. Your job is to learn the secret number by making exactly 6
guesses. You can guess by entering numbers into the "Enter guess" field
and clicking "Guess". The Tool will tell you if the number you guess is
higher or lower than the secret number. When you have the answer, enter
it into the "Final answer" field and click the "Submit answer" button.
: With successive approximation, what is the strategy when making the first guess? For example, if you had a 10 bit ADC, what would be your first guess?
Observation: The speed of a successive approximation ADC relates linearly with its precision in bits.
Normally we don’t specify accuracy for just the ADC, but rather we give the accuracy of the entire system (including transducer, analog circuit, ADC and software). An ADC is monotonic if it has no missing codes as the analog input slowly rises. This means if the analog signal is a slowly rising voltage, then the digital output will hit all values one at a time, always going up, never going down. The figure of merit of an ADC involves three factors:
- precision (number of bits),
- speed (how fast can we sample), and
- power (how much energy does it take to operate).
How fast we can sample involves both the ADC conversion time (how long it takes to convert), and the bandwidth (what frequency components can be recognized by the ADC). The ADC cost is a function of the number and quality of internal components.
Consider an n-bit ADC with a range of 0 to Xmax. Let V be the analog input in volts, and data be the digital output as an integer. Ideally, we expect the resolution to be Xmax/2n. However, for a real ADC, the noise level typically is larger than the ADC resolution. So, when we consider the transfer function of the ADC, it doesn't matter which of the following two equations we use:
data = (V*2n)/Xmax
data = (V*(2n-1))/Xmax
: Assume you have a 6-bit ADC with an input range of 0 to 4V. What will be the digital result of the ADC if the analog input is 1V?
: Assume you have an 8-bit ADC with an input range of 0 to 2V. If the digital result of the ADC were to be 64, what was the analog input voltage?
Quiz 7.2
7.3. Details of the ADC on the MSPM0
Two 12-bit ADCs are built into the MSPM0G3507 microcontroller, called ADC0 and ADC1. You will use Lab 7 uses the ADC to collect data. TExaSdisplay also uses the ADC to implement a voltmeter and oscilloscope. Table 7.3.1 shows the ADC0 register bits required to perform sampling on a single channel. Any bits not specified will read 0. For more complex configurations refer to the specific data sheet. The value in the CLKCFG CLKFREQ and CTL0 will configure the conversion speed. We set bit 1 of CTL0 to enable conversions, and set bit 8 of CTL1 to start a conversion. CTL2 configures the ADC resolution and data format. MEMCTL[0] specifies which channel (pin) is the analog input. Table 7.3.2 shows the mapping between pin and analog channel. Each ADC has 8 possible pins. We set SCOMP0 to 0 to specify 8 clocks periods to sample the analog input prior to conversion. Bit 0 of STATUS will be clear when the conversion is complete. Bits 11-0 of MEMRES[0] will contain the digital result of the conversion.
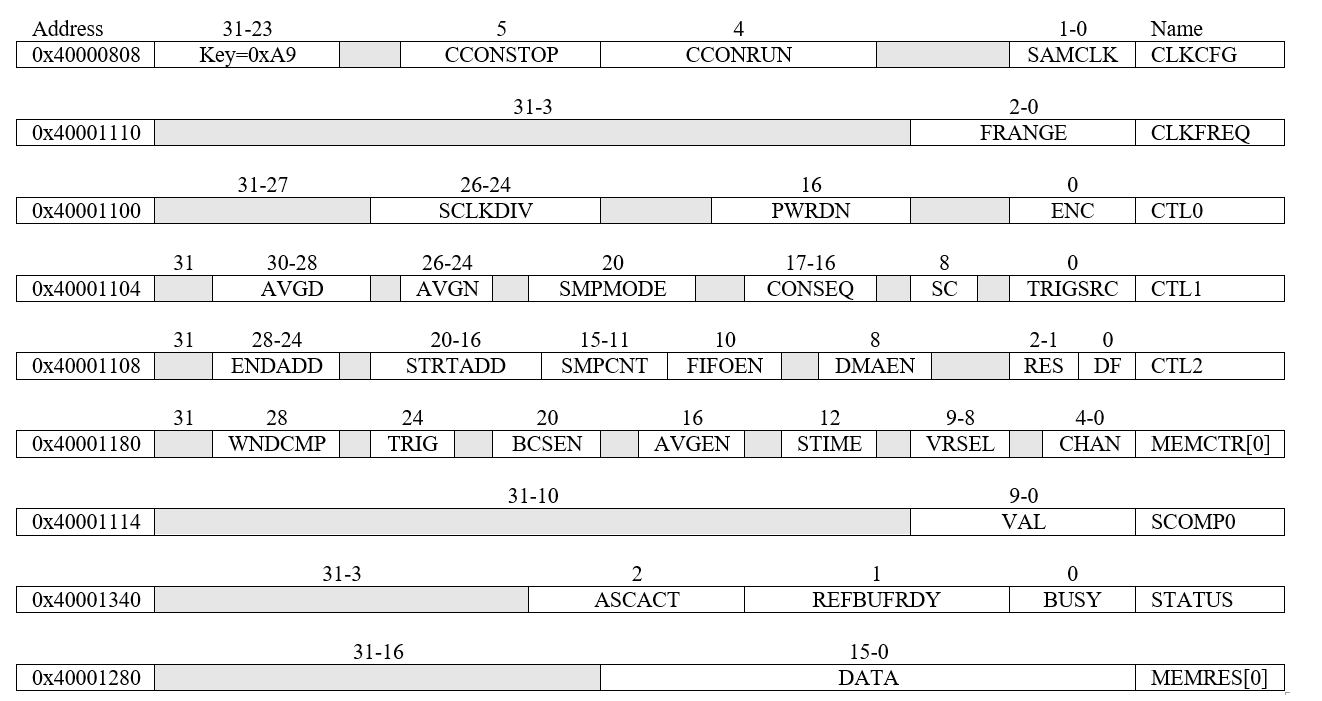
Table 7.3.1. The MSM0 ADC registers. Each register is 32 bits wide.
|
Channel |
ADC0 pin |
ADC1 pin |
0 |
PA27 |
PA15 |
1 |
PA26 |
PA16 |
2 |
PA25 |
PA17 |
3 |
PA24 |
PA18 |
4 |
PB25 |
PB17 |
5 |
PB24 |
PB18 |
6 |
PB20 |
PB19 |
7 |
PA22 |
PA21 |
Table 7.3.2. The MSPM0 has two ADCs, and each ADC supports up to 8 channels.
Program 7.3.1 configures the ADC for software start on one channel. Program 7.3.1 shows a specific details for sampling PB20, which is channel 6 on ADC0. To use ADC1, simply change all the ADC0 to ADC1 in both Programs 7.3.1 and 7.3.2. To sample a different channel, edit step 9 to select the desired sample.
Step 1. We reset the ADC0 module.
Step 2. We activate the ADC0 module.
Step 3. We wait for 24 clocks for the ADC to stabilize.
Step 4. We connect the 40 MHz ULPCLK to the ADC
Step 5. We tell the ADC how fast the processor is running
Step 6. 40MHz/8 means the ADC is clocked at 5 MHz. ENC=0 means off.
Step 7. The mode is no averaging, software trigger, and one sample.
Step 8. CTR2 specifies the digital result is put in MEMRES.
Step 9. We select channel 6 with internal reference.
Step 10. We specify 8 clocks to observe the analog input before conversion.
Step 11. We disable interrupts on ADC.
Observation: The data sheet says the processor clock must be less than or equal to 40 MHz for the ADC to run. We have tested 100 boards so far and all boards allow the ADC to run with a processor clock of 80 MHz.
void ADC0_Init(void){
ADC0->ULLMEM.GPRCM.RSTCTL = 0xB1000003; // 1) reset
ADC0->ULLMEM.GPRCM.PWREN = 0x26000001; // 2) activate
Clock_Delay(24); // 3) wait
ADC0->ULLMEM.GPRCM.CLKCFG = 0xA9000000; // 4) ULPCLK
ADC0->ULLMEM.CLKFREQ = 7; // 5) 40-48 MHz
ADC0->ULLMEM.CTL0 = 0x03010000; // 6) divide by 8
ADC0->ULLMEM.CTL1 = 0x00000000; // 7) mode
ADC0->ULLMEM.CTL2 = 0x00000000; // 8) MEMRES
ADC0->ULLMEM.MEMCTL[0] = 6; // 9) channel 6 is PB20
ADC0->ULLMEM.SCOMP0 = 0; // 10) 8 sample clocks
ADC0->ULLMEM.CPU_INT.IMASK = 0; // 11) no interrupt
}
Program 7.3.1. Initialization of the ADC0 channel 6, PB20, using software start, internal reference, and busy-wait.
Video 7.3.1. ADC Initialization Ritual **needs recording
Program 7.3.2 gives a function that performs an ADC conversion. There are five steps required to perform a software-start conversion. Let V be the analog input voltage in volts. Let data be the digital output of the ADC. The range is 0 to 3.3V. If the analog input is 0, the digital output will be 0, and if the analog input is 3.3V, the digital output will be 4095.
data = (V * 4095) / 3.3V
Step 1. Setting bit 0 of CTL0 enables the ADC.
Step 2. Setting bit 8 of CTL1 starts the ADC.
Step 3. A very short time delay is required for the busy bit to be correct.
Step 4. We wait for busy (bit 0 of CTL0) to be low (not busy).
Step 5. We read the 12-bit digital result.
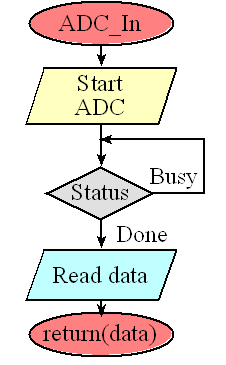
Figure 7.3.3. The software uses busy-wait synchronization.
uint32_t ADC0_In(void){
ADC0->ULLMEM.CTL0 |= 0x00000001; // 1) enable conversions
ADC0->ULLMEM.CTL1 |= 0x00000100; // 2) start ADC
uint32_t volatile delay=ADC0->ULLMEM.STATUS; // 3) time to let ADC start
while((ADC0->ULLMEM.STATUS&0x01)==0x01){} // 4) wait for completion
return ADC0->ULLMEM.MEMRES[0]; // 5) 12-bit result
}
Program 7.3.2. ADC sampling using software start and busy-wait.
Video 7.3.2. Capturing a Sample **needs recording**
It is important to sample the ADC at a regular rate. One simple way to deploy periodic sampling is to perform the ADC conversion in a periodic ISR. In the following code, the sampling rate is determined by the rate of the periodic interrupt. The global variable, Flag is called a semaphore, which is set when new information is stored into the variable Data. We can connect PA0 to a logic analyzer or oscilloscope to verify the sampling rate. The triple toggle allows you to measure the time to execute the ISR and the time between interrupts.
uint32_t Data; // 0 to 4095
uint32_t Flag; // 1 means new data
void SysTick_Handler(void){
GPIOA->DOUTTGL31_0 = 0x01; // toggle PA0
GPIOA->DOUTTGL31_0 = 0x01; // toggle PA0
Data =
ADC0_In(); // Sample ADC
Flag =
1; //
Synchronize with other threads
GPIOA->DOUTTGL31_0 = 0x01; // toggle PA0
}
Program 7.3.3. Real-time data acquisition system.
The main program will initialize Clock, LaunchPad, SysTick, ADC, and enable interrupts. In Figure 7.3.4 configures SysTick to interrupt at 100 Hz. In the main loop, if the semaphore is set, the data is processed and the Flag is cleared. If the semaphore is not set, the main loop can perform other unrelated tasks.
int main(void){
__disable_irq();
LaunchPad_Init(); // resets and activates Port A and Port B
Clock_Init80MHz(0);
ADC0_Init();
SysTick_Init(800000); // Program 5.5.1, 80M/800000 = 100Hz
__enable_irq();
while(1){
if(Flag){
// process data
Flag = 0;
}
}
}
Program 7.3.4. The main program to runs a real-time data acquisition system.
: If the input voltage is 1.65V, what value will the MSPM0 12-bit ADC return?
: If the input voltage is 1.0V, what value will the MSPM0 12-bit ADC return?
: What input voltage exists on the analog pin if the MSPM0 12-bit ADC returns a value of 1024?
: How would we change the four functions in this section to create a data acquistion system using PA15.
: How would we change the four functions in this section to sample at 1 kHz.
Quiz 7.3
7.4. Nyquist Theorem
To collect information from the external world into the computer we must convert it from analog into digital form. This conversion process is called sampling and because the output of the conversion is one digital number at one point in time, there must be a finite time in between conversions, Δt. If we use SysTick periodic interrupts, then this Δt is the time between SysTick interrupts. We define the sampling rate as
fs = 1/Δt
If this information oscillates at frequency f, then according to the Nyquist Theorem, we must sample that signal at
fs > 2f
Furthermore, the Nyquist Theorem states that if the signal is sampled with a frequency of fs, then the digital samples only contain frequency components from 0 to ½ fs. Conversely, if the analog signal does contain frequency components larger than ½ fs, then there will be an aliasing error during the sampling process (performed with a frequency of fs). Aliasing is when the digital signal appears to have a different frequency than the original analog signal.
Discover the
Nyquist Theorem. In this animation, you control the analog signal
by dragging the handle on the left. Click and drag the handle up and
down to create the analog wave (the blue continuous wave). The signal is
sampled at a fixed rate (fs = 1Hz) (the red wave). The
digital samples are connected by straight red lines so you can see the
data as captured by the digital samples in the computer.
|
|
Exercise 1: If you move the handle up and down very slowly you will notice the digital representation captures the essence of the analog wave you have created by moving the handle. If you wiggle the handle at a rate slower than ½ fs, the Nyquist Theorem is satisfied and the digital samples faithfully capture the essence of the analog signal.
Exercise 2: However if you wiggle the handle quickly, you will observe the digital representation does not capture the analog wave. More specifically, if you wiggle the handle at a rate faster than ½ fs the Nyquist Theorem is violated causing the digital samples to be fundamentally different from the analog wave. Try wiggling the handle at a fast but constant rate, and you will notice the digital wave also wiggles but at an incorrect frequency. This incorrect frequency is called aliasing.
If fs=2000 Hz, we will properly sample signals from 0 up to but not including 1000 Hz (0 ≤ f < 1000 Hz). Figure 7.4.1 shows what happens sampling is proper. Figure 7.4.2 shows what happens when the Nyquist Theorem is violated. In both cases a signal was sampled at 2000 Hz (every 0.5 ms). The 200 Hz signal in Figure 7.4.1 is properly sampled, which means the digital samples accurately describe the analog signal. However, in Figure 7.4.2, the 2200 Hz signal is not sampled properly, which means the digital samples do not accurately describe the analog signal. This error is called aliasing. Aliasing occurs when the input signal oscillates faster than the sampling rate and it characterized by the digital samples “looking like” it is oscillating at a different rate than the original analog signal. For these two sets of sampled data, notice the digital data are exactly the same.
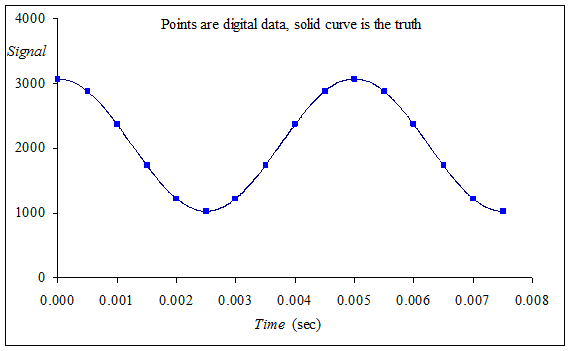
Figure 7.4.1. The signal is 200 Hz, sampling rate is 2000 Hz.
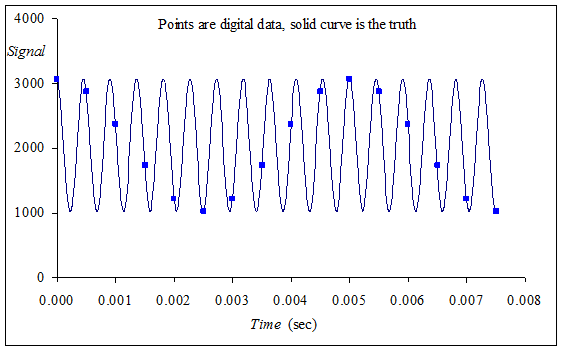
Figure 7.4.2. Aliasing occurs when the input analog signal oscillates faster (2200 Hz) than the rate of the ADC sampling (2000Hz).
Video 7.4.1. Aliasing Demonstration: The Wagon Wheel Effect
: Assume you wish to represent sounds in digital form on the computer, either as inputs sampled from an ADC, or as outputs created with a DAC. The approximate range of canine hearing is 40 to 60 kHz. What sampling rate preverves all information for canine sound?
: The sounds in Lab 9 are sampled at 11 kHz. What range of frequencies can exist in the samples?
: Assume the input is a pure sine wave at 1 kHz, 1.65+1*sin(2*pi*1k*t), and the ADC is sampled at 2 kHz. Will the information be properly represented in the digital data?
Valvano Postulate: If fmax is the largest frequency component of the analog signal, then you must sample more than ten times fmax in order for the reconstructed digital samples to look like the original signal when plotted on a voltage versus time graph.
Quiz 7.4
7.5. Central Limit Theorem
The resolution of a measurement system is the smallest change in input that can be reliably detected. The accuracy of a measurement system is the average difference between measured value and truth. For most systems, resolution and accuracy are dominated by noise, rather than the precision of the ADC. To improve signal to noise ratio, we can sample the ADC multiple times and average the samples.
Assume the true signal is μ. More
formally, μ is the expected value of the signal. When we
sample the signal, noise is added, so the sampled data does not equal
the truth. Let x1, x2, x3,... be sampled data on
the same true signal. To use the Central Limit Theorem (CLT)
we will make the following assumptions:
1) the added noise is independent (the added noise of one
sample is not related to the added noise of another sample);
2) the added noise has the same probability distribution
(whatever physical process that generated the noise in one sample,
creates noise in the other samples);
The CLT states that if you have a signal with mean μ and
standard deviation σ and take sufficiently large random
samples (n>30), and calculate the average
X = (sum(x1+x2+...+xn))/n
then the distribution of X will be approximately normally
distributed (Gaussian). More importantly, the expected value of X
will approach μ. If the noise has zero mean (equally likely
to be additive as subtractive), then X will approach the true
signal as n increases. One estimate of noise is the standard
deviation of multiple samples.
S = sqrt((sum((x1-X)^2+(x2-X)^2+...+(xn-X)^2))/n)
There are two approaches to averaging on the MSPM0. First, there is a mode on the ADC
to automatically take multiple samples and
return the average. For more details in this mode see the
ADC0_InitAve function in the ADC.c file,
which can be found in the inc folder as part of the installation package.
Second, we can write software to sample multiple times and perform
the averaging in software. Program 7.5.1 shows one approach
to software averaging.
uint32_t Sample(uint32_t n){
uint32_t sum = 0;
for(int j=0; j<n; j++){
sum += ADCin();
}
return sum/n; // averaging
}
Program 7.5.1. The main program to runs a real-time data acquisition system.
You will notice the signal to noise ratio will improve dramatically if you use averaging. However, the disadvantage of averaging is the time to convert. If taking one sample takes 8us, then activating 32-point averaging will increase the time to sample to 32*8=128us. Similarly, it will take more electrical power to deploy averaging.
Video 7.5.1 Central Limit Theorem
Because of noise, if we set the ADC input to a constant voltage, and call Sample many times, we will get a distribution of digital outputs. We plot the number of times we got an output as a function of the output sample. The shape of this response is called a probability mass function (pmf) characterizing the noise processes. A pmf plots the number of occurrences versus the ADC sample value. To illustrate the CTL, 1.65V was connected to an analog pin and Program 7.5.1 was called 1000 times. The experiment was performed at three values of n=1 (no averaging), n=4, and n=16. Notice the shape becomes Gaussian and the standard deviation reduces. In particular, the data with 1 point (no averaging) has two or three humps (not normally distributed), but with 16-point average there is one symmetric hump (normally distributed)
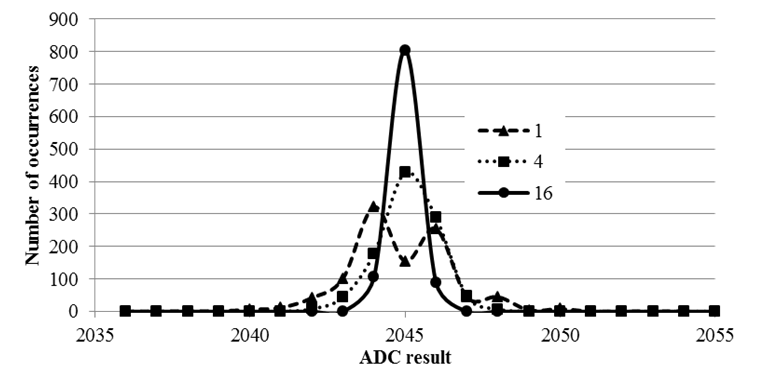
Figure 7.5.1. Probability mass functions showing hardware averaging improves signal to noise ratio.
: Give an advantage of using averaging.
: Give two disadvantages of using averaging.
: The MSPM0 has hardware averaging. What would you do if you want to deploy averaging, but you are using a different microcontroller that does not support hardware averaging?
Quiz 7.5
7.6. C++ on the MSPM0, ECE319H only
In most aspects, running C++ on the microcontroller is identical to running C++ on other machines. However, be aware of the memory limitations of the TM4C123. To run C++ we will create a small heap and continue to have a small stack, knowing that all globals, statics, locals, and heap must fit into the 32 kibibytes of RAM on the TM4C123. The following code exists in the startup file for Lab7_C++ project, creating 1024 bytes of stack and 512 bytes of heap.
Stack_Size EQU 0x00000400
AREA STACK, NOINIT, READWRITE, ALIGN=3
Stack_Mem SPACE Stack_Size
__initial_sp
; Heap Configuration
Heap_Size EQU 0x00000200
AREA HEAP, NOINIT, READWRITE, ALIGN=3
__heap_base
Heap_Mem SPACE Heap_Size
__heap_limit
Video 7.6.1. Running C++ on the MSPM0. **needs recording**
Video 7.6.2. Running a vector.cpp C++ example from EE312H on the MSPM0. **needs recording**
7.7. Periodic Interrupt using Timers
The MSPM0G3507 microcontroller has 7 timers, which can be used to create periodic interrupts. Timer G12 is a 32-bit hardware timer with no prescale; the other six are 16-bit timers with 8-bit prescale. Each timer has a counter register, e.g., TIMG0->COUNTERREGS.CTR, which is incremented or decremented automatically in hardware. In periodic timer mode, the CTR register continuously counts down. Timers G0 and G8 are clocked at one half the bus frequency. Timers A0, A1, G6, G7, and G12 are clocked at the bus frequency. All timers except G12 have a clock prescale=CPS register containing an 8-bit prescale. If the bus clock period is Δt, then the timer counting period is
Δt*(CPS+1)*2 for G0 and G8
Δt*(CPS+1) for A0, A1, G6, G7, and G12
If we make the CPS=39 with a bus clock at 80 MHz, then Timer G0 counts down at 1 MHz (every 1us). Each timer also has a LOAD register, which is a 32-bit constant on G12 and 16-bit on the other six timers. When the timer counts from 1 to 0 it sets the trigger flag, which is bit 0 in the RIS register. On the next count, the CTR register is reloaded with the value in LOAD. In periodic mode, the CTR register continuously counts
LOAD, LOAD-1, LOAD-2,...2, 1, 0, LOAD, LOAD-1, LOAD-2,...
Therefore, the interrupt will occur every
Δt*(CPS+1)(LOAD+1)*2 for G0 and G8
Δt*(CPS+1)(LOAD+1) for A0, A1, G6, and G7
Δt*(LOAD+1) for G12
In periodic mode, the timer runs continuously. The timers can be used to create pulse width modulated outputs and measure pulse width, period, or frequency. Program 7.4.1 shows how to use Timer G0 to trigger a periodic interrupt. With a bus clock of 80MHz, Timer G0 is clocked at 40MHz (25ns period). The slowest we could interrupt is if we set LOAD=0xFFFF and CPS=0xFF. At these settings, Timer G0 will interrupt every 25ns*256*65536 = 419.4304ms.
During initialization, we first reset and activate the timer. After a short delay, we set CLKSEL=0x08 and CLKDIV=0 to clock the timer from the bus clock. On G0 and G8 the timer will clock at 1/2 bus frequency. Next, we set the CPS and LOAD to specify the interrupt period. We set CTRCTL=0x02 to specify continuous down counting. We set bit 0 of IMASK to arm the periodic interrupt. We set bit 0 of CCLKCTL to enable the timer. Timer G0 is interrupt 16, so we enable Timer G0 interrupts by setting bit 16 in NVIC->ISER[0]. Remember NVIC->ISER[0] is a write 1 to set, but writing zeros has no effect on this register. Therefore, NVIC->ISER[0]=1<<16; is friendly. The priority bits for Timer G0 are bits 7-6 in NVIC->IP[4]. The last step is to enable the timer by setting bit 0 of CTRCTL.
The interrupt trigger flag is bit 0 of the RIS register. There are two ways the ISR can clear the trigger flag:
- Write 1 to the TIMG0->CPU_INT.ICR register
- Read the TIMG0->CPU_INT.IIDX register (which will return a 1)
Note also, TIMG0->CPU_INT.ICR is write 1 to clear, so,
TIMG0->CPU_INT.ICR=1; is friendly way clear bit 0 of RIS.
void TimerG0_IntArm(uint16_t period, uint32_t prescale, uint32_t priority){
TIMG0->GPRCM.RSTCTL = 0xB1000003;
TIMG0->GPRCM.PWREN = 0x26000001;
Clock_Delay(24); // time for TimerG0 to power up
TIMG0->CLKSEL = 0x08; // bus clock
TIMG0->CLKDIV = 0x00; // divide by 1
TIMG0->COMMONREGS.CPS = prescale-1; // divide by prescale,
TIMG0->COUNTERREGS.LOAD = period-1; // set reload register
TIMG0->COUNTERREGS.CTRCTL = 0x02;
// bits 5-4 CM =0, down
// bits 3-1 REPEAT =001, continue
// bit 0 EN enable (0 for disable, 1 for enable)
TIMG0->CPU_INT.IMASK = 1; // zero event mask
TIMG0->COMMONREGS.CCLKCTL = 1;
NVIC->ISER[0] = 1 << 16; // TIMG0 interrupt
NVIC->IP[4] = (NVIC->IP[4]&(~0x000000FF))|(priority<<6); // set priority (bits 7,6) IRQ 16
TIMG0->COUNTERREGS.CTRCTL |= 0x01;
}
uint32_t count;
int main(void){
__disable_irq();
Clock_Init80MHz(0);
count=0;
LaunchPad_Init();
TimerG0_IntArm(10000,40,2); // 40MHz/40/10000 = 100Hz
__enable_irq();
while(1){
GPIOA->DOUTTGL31_0 = RED1;
}
}
void TIMG0_IRQHandler(void){
if((TIMG0->CPU_INT.IIDX) == 1){ // this will acknowledge
GPIOB->DOUTTGL31_0 = GREEN; // toggle PB27
count++;
}
}
Program 7.7.1. Periodic interrupts using Timer G0 .
Video 7.7.1. TimerG0 **needs recording**
Observation: If we set LOAD=0, the counter can never go from 1 to 0, so the interrupt flag will never be set. I.e., LOAD=0 is one way to halt the interrupts.
Quiz 7.7
7.8. ECE319K Lab 7 videos
Educational Objectives of Lab 7
• Sampling
— ADC conversion
— Interrupt-driven periodic sampling
— Calibration and accuracy
— Nyquist Theorem
— Central Limit Theorem
• Thread synchronization
— Mail box
• Fixed-point numbers
— Value = Integer*Constant
• Modular development
• Object oriented design in C++ (EE319H)
Lab7 Introduction
In this video we review the software starter project and overview the design steps for implementing Lab 7. The full scale range of the measurement is determined by the physical size of the potentiometer (some move 0 to 1.5cm, and others move 0 to 2.0cm).
Video 7.8.1. Lab 7 Starter Project
Lab7 SlidePot
We show how to attach slide pot to protoboard. This slide potentiometer has a range of 0 to 2 cm.
Lab7 Calibration
In this video we demonstrate the steps to calibrate the device. We activate hardware averaging to improve signal to noise ratio
Video 7.8.3. Lab 7 Calibration
Lab7 Accuracy
In this video we demonstrate the steps to determine accuracy of the device. We will also show you how to estimate resolution. We activate hardware averaging to improve signal to noise ratio.
Collect two to five measurements with your distance measurement system. In the left column place the true distances as determined by your eyes looking at the cursor and the ruler. In the right column place the measured distances as determined by your system. When you have entered at least two sets of data, click the "Calculate" button.
True values | Measured values | Errors
The number of data sets is
The maximum error is
The average error is
Lab7 Demo
Demonstration of Lab 7 final solution
Video 7.8.5. Lab 7 Demonstration
7.9. Robot Car Controller, optional forECE319K/ECE319H
The goal is to drive a robot car autonomously down a road. Autonomous driving is a difficult problem, and we have greatly simplified it and will use this simple problem to illustrate the components of a control system. Every control system has real-world parameters that it wishes to control. These parameters are called state variables. In our system we wish to drive down the middle of the road, so our state variables will be the distance to the left side of the road and the distance to the right side of the road as illustrated in Figure 7.9.1. When we are in the middle of the road these two distances will be equal. So, let’s define Error as:
Error = Dleft – Dright
If Error is zero we are in the middle of the road, so the controller will attempt to drive the Error parameter to zero.
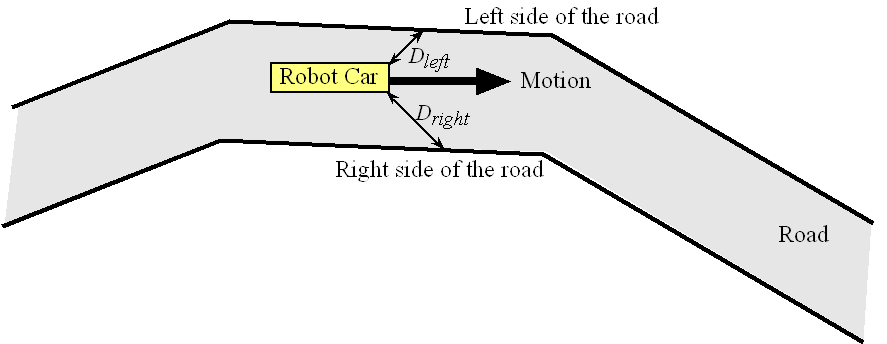
Figure 7.9.1. Physical layout of the autonomous robot as is drives down the road.
Video 7.9.1a. IR Sensor for Robot Car
We will need sensors and a data acquisition system to measure Dleft and Dright. In order to simplify the problem we will place pieces of wood to create walls along both sides of the road, and make the road the same width at all places along the track. The Sharp GP2Y0A21YK0F infrared object detector can measure distance (http://www.sharpsma.com) from the robot to the wood. This sensor creates a continuous analog voltage between 0 and +3V that depends inversely on distance to object, see Figure 7.1.5. We will avoid the 0 to 10 cm range where the sensor has the nonmonotonic behavior. We will use two ADC channels (PE4 and PE5) to convert the two analog voltages to digital numbers. Let Left and Right be the ADC digital samples measured from the two sensors. We can assume distance is linearly related to 1/voltage, we can implement software functions to calculate distance in mm as a function of the ADC sample (0 to 4095). The 241814 constant was found empirically, which means we collected data comparing actual distance to measured ADC values.
Dleft = 241814/Left
Dright = 241814/Right
Figure 7.9.2 shows the accuracy of this data acquisition system, where the estimated distance, using the above equation, is plotted versus the true distance.
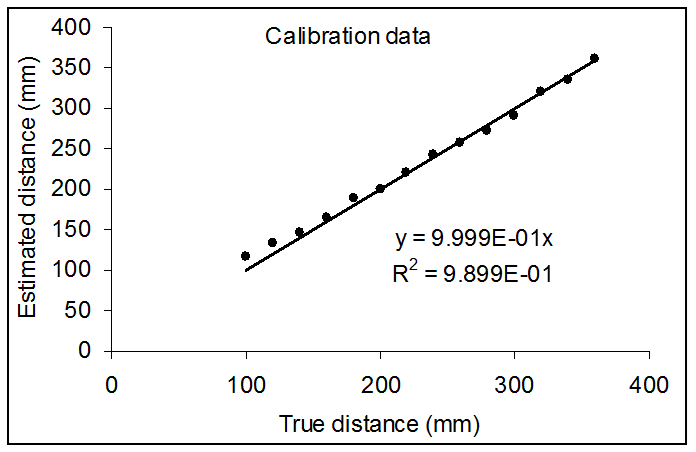
Figure 7.9.2. Measurement accuracy of the Sharp GP2Y0A21YK0F distance sensor used to measure distance to wall.
Next we need to extend the robot built in Example 12.2. First we build two motor drivers and connect one to each wheel, as shown in Figure 7.9.3. There will be two PWM outputs: PA6 controls the right motor attached to the right wheel, and PA5 controls the left motor attached to the left wheel. The motors are classified as actuators because they exert force on the world. Similar to Example 12.2 we will write software to create two PWM outputs so we can independently adjust power to each motor. If the friction is constant, the resistance of the motor, R, will be fixed and the power is
Power = (8.42/R)*H/(H+L)
When creating PWM, the period (H+L) is fixed and the duty cycle is varied by changing H. So we see the robot controller changes H, it has a linear effect on delivered power to the motor.
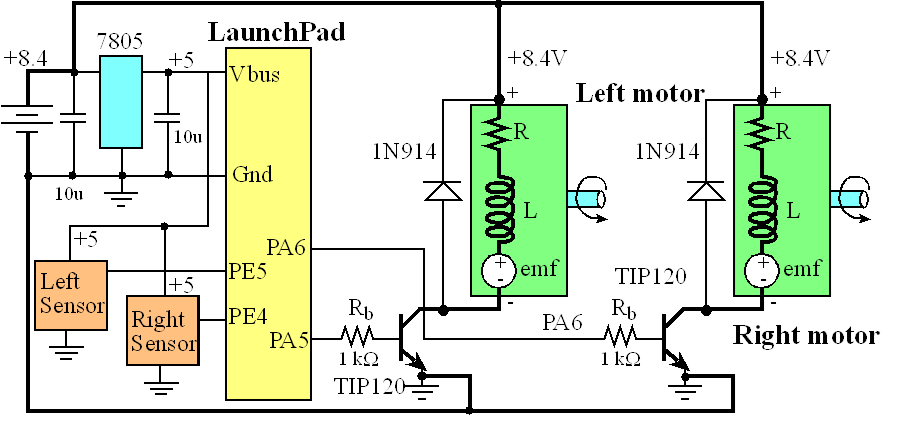
Figure 7.9.3. Circuit diagram of the robot car. One motor is wire reversed from the other, because to move forward one motor must spin clockwise while the other spins counterclockwise.
The currents can range from 500mA to 1 A, so TIP120 Darlington transistors are used, because they can sink up to 3 A see data sheet. Notice the dark black lines in Figure 7.9.3; these lines signify the paths of these large currents. Notice also the currents do not pass into or out of the LaunchPad. Figure 7.9.4 shows the robot car. The two IR sensors are positioned in the front at about 45 degrees.
Video 7.9.2. Autonomous Robot Demonstration
Figure 7.9.4 illustrates the feedback loop of the control system. The state variables are Dleft and Dright. The two sensors create voltages that depend on these two state variables. The ADC samples these two voltages, and software calculates the estimates Dleft and Dright. Error is the difference between Dleft and Dright. The right motor is powered with a constant duty cycle of 40%, while the duty cycle of the left motor is adjusted in an attempt to drive down the middle of the road. We will constrain the duty cycle of the left motor to between 30% and 50%, so it doesn’t over compensate and spin in circles. If the robot is closer to the left wall (Dleft < Dright) the error will be negative and more power will be applied to the left motor, turning it right. Conversely, if the robot is closer to the right wall (Dleft > Dright) the error will be positive and less power will be applied to the left motor, turning it left. Once the robot is in the middle of the road, error will be zero, and power will not be changed. This control algorithm can be written as a set of simple equations. The number “200” is the controller gain and is found by trial and error once the robot is placed on the road. If it is slow to react, then we increase gain. If it reacts too quickly, we decrease the gain.
Error = Dleft - Dright
LeftH = LeftH – 200*Error;
if(LeftH < 30*800) LeftH=30*800; // 30% min
if(LeftH > 50*800) LeftH=50*800; // 50% max
LeftL = 80000 - LeftH; // constant period
Observation: In the field of control systems, a popular approach is called PID control, which stands for proportional integral derivative. The above simple algorithm actually implements the integral term of a PID controller. Furthermore, the two if statements in the control software implement a feature called anti-reset windup.
These controller equations are executed in the SysTick ISR so the controller runs at a periodic rate.
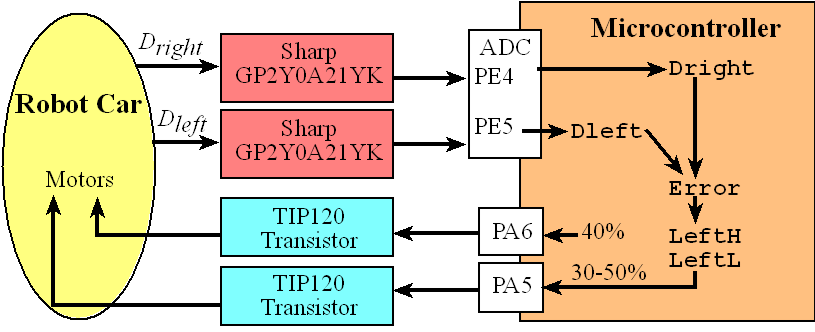
Figure 7.9.4. Block diagram of the closed loop used in the robot car.
Video 7.9.3. The Robot Control System
Details about microcontroller-based control systems can be found in Chapter 10 of Embedded Systems: Real-Time Operating Systems for ARM® Cortex-M Microcontrollers, 2022, ISBN: 978-1466468863.
Bill of Materials
1) Two DC geared motors, HN-GH12-1640Y,GH35GMB-R, Jameco Part no.
164786
- 0.23in or 6 mm shaft (get hubs to match)
2) Metal or wood for base,
3) Hardware for mounting
- 2 motor mounts 1-1/4 in. PVC Conduit Clamps Model #
E977GC-CTN Store SKU # 178931 www.homedepot.com
- some way to attach the LaunchPad (I used an Erector
set, but you could use rubber bands)
4) Two wheels and two hubs to match the diameter of the motor shaft
- Shepherd 1-1/4 in. Caster Rubber Wheel Model # 9487
www.homedepot.com
- 2 6mm hubs Dave's Hubs - 6mm Hub Set of Two Part#
0-DWH6MM www.robotmarketplace.com
- 2 3-Inch Diameter Treaded Lite Flite Wheels 2pk
Part# 0-DAV5730 www.robotmarketplace.com
5) Two GP2Y0A21YK IR range sensors
- Sparkfun, www.sparkfun.com SEN-00242 or
http://www.parallax.com/product/28995
6) Battery
- 8.4V NiMH or 11.1V LiIon. I bought the 8.4V NiMH batteries you see in
the video as surplus a long time ago. I teach a real-time OS class where
students write an OS then deploy it on a robot. I have a big pile of
these 8.4V batteries, so I used a couple for the two robots in this
class. NiMH are easier to charge, but I suggest Li-Ion because they
store more energy/weight. For my medical instruments, I use a lot of
Tenergy 31003 (7.4V) and Tenergy 31012 (11.1V) (internet search for the
best price). You will need a Li-Ion charger. I have used both of these
Tenergy TLP-4000 and Tenergy TB6B chargers.
7) Electronic components
- two TIP120 Darlington NPN transistors
-2 1N914 diodes
-2 10uF tantalum caps
- 7805 regular
-2 10k resistors
Websites to buy robot parts
Robot parts
Pololu Robots
and Electronics
Robot
Marketplace
Sparkfun
Parallax
Tower Hobbies
Full-service parts
Newark (US)
or element14
(worldwide)
Digi-Key
Mouser
Jameco
Part search engine
Go to Chapter 8: Serial Communication
This material was created to teach ECE319K at the University of Texas at Austin
Reprinted with approval from Introduction to Embedded Systems Using the MSPM0+, ISBN: 979-8852536594

Embedded
Systems - Shape the World by Jonathan Valvano and Ramesh Yerraballi is
licensed under a Creative
Commons
Attribution-NonCommercial-NoDerivatives 4.0 International License.
Based on a work at http://users.ece.utexas.edu/~valvano/mspm0/