Department of Electrical and Computer Engineering
The University of Texas at Austin
EE 306, Fall 2002
Yale Patt, Instructor
TAs: Asad Bawa, Linda Bigelow, Mustafa Erwa, Lester Guillory, Kevin Major,
Moinuddin Qureshi, Paroma Sen, Tanay Shah, Santhosh Srinath,
Matt Starolis, David Thompson, Vikrant Venkateshwar
Problem Set #3
Due: Monday, September 30, 2002 before class
1) Problem 12 from PS 2
2) Do Problem 12 from PS 1 with the following hexadecimal representation: x8A424954.
3) Textbook Problem 3.16 (unmodified)
Implement the following functions using AND, OR, and NOT logic gates. The inputs are A, B, and the output is F.
a) F has the value 1 only if A has the value 0 and B has the value 1.
b) F has the value 1 only if A has the value 1 and B has the value 0.
c) Use your answers from (a) and (b) to implement a one-bit adder. The truth table for the one-bit adder is given below.
| A |
B |
Sum |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
d) Is it possible to create a four-bit adder (a circuit that will correctly add two 4-bit quantities) using only four copies of the logic diagram from (c)? If not, what information is missing? Hint: When A = 1 and B = 1, a sum of 0 is produced. What information is disregarded?
4) Textbook Problem 3.17 (modified)
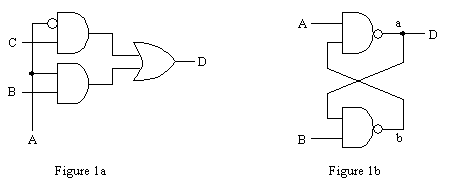
The logic circuit in Figure 1a has inputs A, B, C. The logic circuit in Figure 1b has inputs A and B. Both logic circuits have an output D.
a) For the logic circuit in Figure 1a, fill in the truth table for the output value D.
| A |
B |
C |
D |
| 0 | 0 | 0 | |
| 0 | 0 | 1 | |
| 0 | 1 | 0 | |
| 0 | 1 | 1 | |
| 1 | 0 | 0 | |
| 1 | 0 | 1 | |
| 1 | 1 | 0 | |
| 1 | 1 | 1 | |
b) For the logic circuit in Figure 1b, fill in the truth table for the output value D. In this case, A, B, a, and b specify the current state of the logic circuit, and D is the next state of a (in other words, the value of a some time after A and B have been applied). Three lines have been done for you as an example.
| A |
B |
a |
b |
D |
| 1 | 1 | 0 | 1 | |
| 1 | 1 | 1 | 0 | |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | |
| 0 | 1 | 0 | 1 | |
| 0 | 1 | 1 | 0 | |
| 0 | 0 | 0 | 1 | ? |
| 0 | 0 | 1 | 0 | ? |
The last two lines have been filled in for you. You do not have to work them out.
c) There is a fundamental difference between the behavioral characteristics of these two circuits. What is it? Hint: What happens when the voltage at input A goes from 0 to 1 in both circuits?
5) Textbook Problem 3.21 (unmodified)
Say the speed of a logic structure depends on the largest number of logic gates through which any of the inputs must propagate to reach an output. Assume that a NOT, an AND, and an OR gate all count as one gate delay. For example, the propagation delay for a two-input decoder shown in Figure 3.11 (page 56) is 2 because some inputs propagate through two gates.
a) What is the propagation delay for the two-input mux shown in Figure 3.12 (page 57)?
b) What is the propagation delay for the one-bit full adder in Figure 3.15 (page 59)?
c) What is the propagation delay for the four-bit adder shown in Figure 3.16 (page 59)?
d) What if the four-bit adder were extended to 32 bits?
6) Textbook Problem 3.25 (unmodified)
If a computer has eight-byte addressability and needs three bits to access a location in memory, what is the total size of memory in bytes?
7) Textbook Problem 3.26 (modified)
Using Figure 3.20 (page 65), the diagram of the four-entry, three-bit memory,
a) To read from the second from the top memory location, what must the values of A[1:0] and WE be?
b) To write to the third from the top memory location, what must the values of A[1:0] and WE be?
c) To change the number of entries in the memory from 4 to 120, how many total address lines would be needed? If we keep the number of bits in each entry unchanged, what would be the addressability of the memory after this change was made?
d) Suppose the minimum width (in bits) of the program counter (the program counter is a special register within a CPU, and we will discuss it in detail in the next chapter) is the minimum number of bits needed to address all 120 locations in our memory from part (c). How many additional memory locations could be added to this memory without having to alter the width of the program counter?
8) Textbook Problem 3.28 (modified)
a) Generate the gate-level logic that implements the following truth table.
b) From the gate-level structure from part (a), generate a transistor diagram that implements the logic structure.
| in0 |
in1 |
f(in0, in1) |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
9) Fill in the truth table for the master-slave flip flop in Figure 2. Inputs A, B, D, and Clock specify the current state of the flip flop, and outputs B+ and D+ are the next states of B and D, respectively. Three lines have been done for you as an example.
| A |
B |
D |
Clock |
B+ |
D+ |
| 0 | 0 | 0 | 0 | | |
| 0 | 0 | 0 | 1 | | |
| 0 | 0 | 1 | 0 | | |
| 0 | 0 | 1 | 1 | | |
| 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | | |
| 0 | 1 | 1 | 0 | | |
| 0 | 1 | 1 | 1 | | |
| 1 | 0 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | | |
| 1 | 0 | 1 | 0 | | |
| 1 | 0 | 1 | 1 | | |
| 1 | 1 | 0 | 0 | | |
| 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | | |
| 1 | 1 | 1 | 1 | | |
a) What happens when the Clock signal is 0?
b) What happens when the Clock signal is 1?
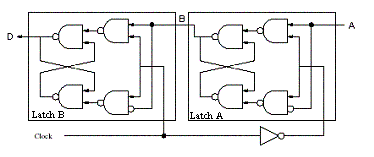
Figure 2
10) IEEE sells cokes for 35 cents. Suppose they install a coke controller that only takes the following three inputs: nickel, dime, and quarter. After you put in each coin, you push a pushbutton to register the coin. If at least 35 cents has been put in the controller, it will output a coke and proper change (if applicable). Draw a finite state machine that describes the behavior of the coke controller. Each state will represent how much money has been put in (Hint: There will be seven of these states). Once enough money has been put in, the controller will go to a final state where the person will receive a coke and proper change (Hint: There are five such final states). From the final state, the next coin that is put in will start the process again.

