Chapter
14: Analog to Digital Conversion, Data Acquisition and Control
Modified to be compatible with EE319K Lab 8
Jonathan Valvano and Ramesh Yerraballi
Throughout this course we have seen that an embedded system uses its input/output devices to interact with the external world. In this chapter we will focus on input devices that we use to gather information about the world. More specifically, we present a technique for the system to measure analog inputs using an analog to digital converter (ADC). We will use periodic interrupts to sample the ADC at a fixed rate. We define the rate at which we sample as the sampling rate, and use the symbol fs. We will then combine sensors, the ADC, software, PWM output and motor interfaces to implement intelligent control on our robot car.
|
Learning Objectives:
|
Video 14.0. Introduction to Digitization |
Video 14.1. Digitization Concepts.
The measurand is a real world signal of interest like sound, distance, temperature, force, mass, pressure, flow, light and acceleration. Figure 14.1 shows the data flow graph for a data acquisition system or control system. x(t) is the time-varying signal we are attempting to measure. The control system uses an actuator to drive a measurand in the real world to a desired value while the data acquisition system has no actuator because it simply measures the measurand in a nonintrusive manner. Consider an entire system that collects data, not just the ADC. The following four limitations exist when sampling data.
Amplitude resolution is the smallest change in input signal that can be distinguished. For example, we might specify the resolution as dX. Amplitude range is defined as the smallest to largest input value that can be measured. For example, we might specify the range as Xmin to Xmax. Amplitude precision is defined as the number of distinct values from which the measurement is selected. The units of precision are given in alternative or bits. If a system has 12-bit precision, there are 2^12 or 4096 distinct alternatives. For example if we use a slide pot to measure distance, the range of that pot might be 0 to 1.5cm. If there is no electrical noise and we use a 12-bit ADC, then the theoretical resolution is 1.5cm/4095, or about 0.0004 cm. In most systems, the resolution of the measurement is determined by noise and not the number of bits in the ADC. Time quantization is the time difference between one sample and the next. Time interval is the smallest to largest time during which we collect samples. If we use a 10-Hz SysTick interrupt to sample the ADC and calculate distance, the sampling rate, fs, is 10 Hz, and the time quantization is 1/fs=0.1 sec. If we use a memory buffer with 500 elements, then the time interval is 0 to 50 sec.
: Assume Xmin, Xmax, and dX are all given in the same units. Give a formula that relates the precision in bits as a function of Xmin, Xmax and dX.
: Assume the precision is n in bits, and Xmin, Xmax, and dX are all given in the same units. Give a formula that relates the resolution, dX as a function of Xmin, Xmax and n.
: Assume you have a 12-bit ADC and store data into an array of type uint16_t. Let fs be the sampling rate in Hz, and T be the total time interval required to collect samples in sec. Give a formula that relates needed memory in bytes as a function of fs and T.
: Assume you have an 8-bit ADC. Let the sampling rate be 100 Hz. Assume you allocate 20,000 out of the available 32,768 bytes of RAM to store the data. What is the corresponding time interval? I.e., how many seconds of data can you record?
: Assume you have a 4-bit DAC used to play sound. Let the sampling rate be 11 kHz. You can pack two DAC samples into one byte. Assume you allocate 128 kibibytes out of the available 256 kibibytes of ROM to store the data. What is the corresponding time interval? I.e., how many seconds of sound can you play?
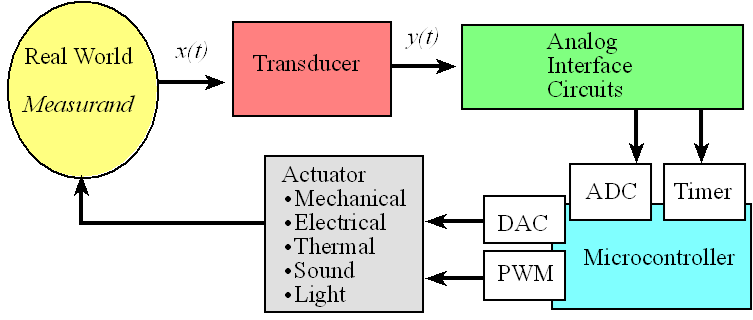
Figure 14.1. Signal paths a data acquisition system.
The input or measurand is x. The output is y. A transducer converts x into y. A wide variety of inexpensive sensors can be seen at https://www.sparkfun.com/categories/23 Examples include
· Sound Microphone
· Pressure, mass, force Strain gauge, force sensitive resistor
· Temperature Thermistor, thermocouple, integrated circuits
· Distance Ultrasound, lasers, infrared light
· Flow Doppler ultrasound, flow probe
· Acceleration Accelerometer
· Light Camera
· Biopotentials Silver-Silver Chloride electrode
A linear transducer is an input/output function fits a straight line. In other words, the input/output response fits a linear equation:
y = m*x*b
where m and b are constants. Software will have an easy time with a linear transducer. For example, the linear potentiometer, PTA20432015CPB10, has a transfer function as shown in Figure 14.2, where the input x is distance in cm, and the output y is resistance in kΩ. You can use a simple circuit to convert resistance to voltage, the ADC to convert voltage to an integer, and simple software to convert an integer to distance.

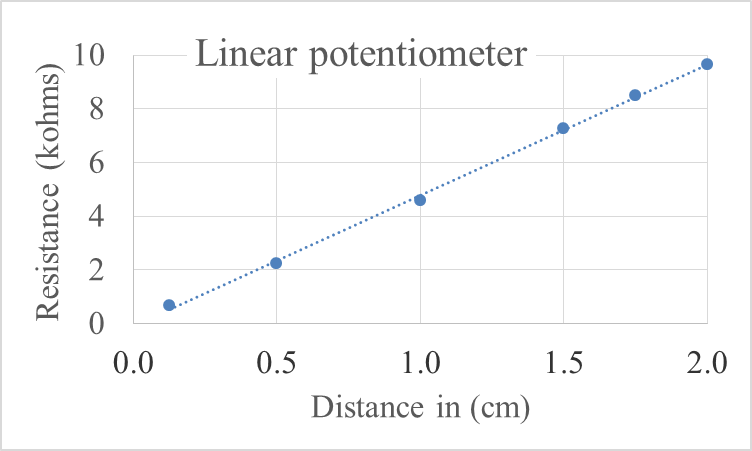
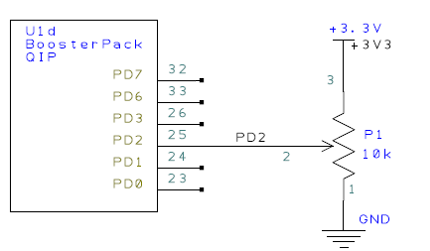
Figure 14.2. The linear potentiometer distance sensor exhibits linear behavior.
: Consider the linear potentiometer in Figure 14.2. Let x be the distance in cm and let y be the resistance in kohm. Give an appropriate transfer function showing y as a function of x.
A nonmonotonic transducer is an input/output function that does not have a mathematical inverse. For example, if two or more input values yield the same output value, then the transducer is nonmonotonic. Software will have a difficult time correcting a nonmonotonic transducer. For example, the Sharp GP2Y0A21YK IR distance sensor has a transfer function as shown in Figure 14.3. If you read a transducer voltage of 2 V, you cannot tell if the object is 3 cm away or 12 cm away. However, if we assume the distance is always greater than 10cm, then this transducer can be used. Details about transducers and actuators can be found in Embedded Systems: Real-Time Interfacing to ARM Cortex-M Microcontrollers, 2020, ISBN: 978-1463590154.

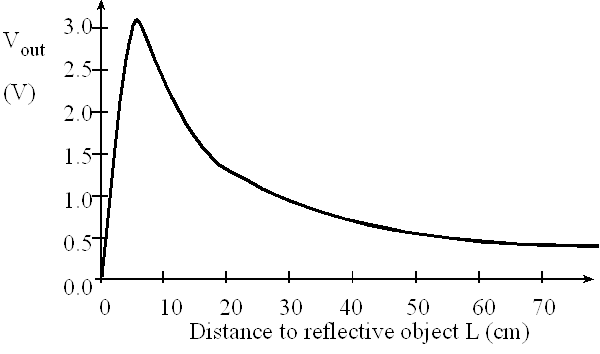
Figure 14.3. The Sharp IR distance sensor exhibits nonmonotonic behavior.
14.2. The Analog to Digital Converter
An analog to digital converter (ADC) converts an analog signal into digital form, shown in Figure 14.4. An embedded system uses the ADC to collect information about the external world (data acquisition system.) The input signal is usually an analog voltage, and the output is a binary number. The ADC precision is the number of distinguishable ADC inputs (e.g., 4096 alternatives, 12 bits). The ADC range is the maximum and minimum ADC input (e.g., 0 to +3.3V). The ADC resolution is the smallest distinguishable change in input (e.g., 3.3V/4095, which is about 0.81 mV). The resolution is the change in input that causes the digital output to change by 1.
Range(volts) = Precision(alternatives) • Resolution(volts)
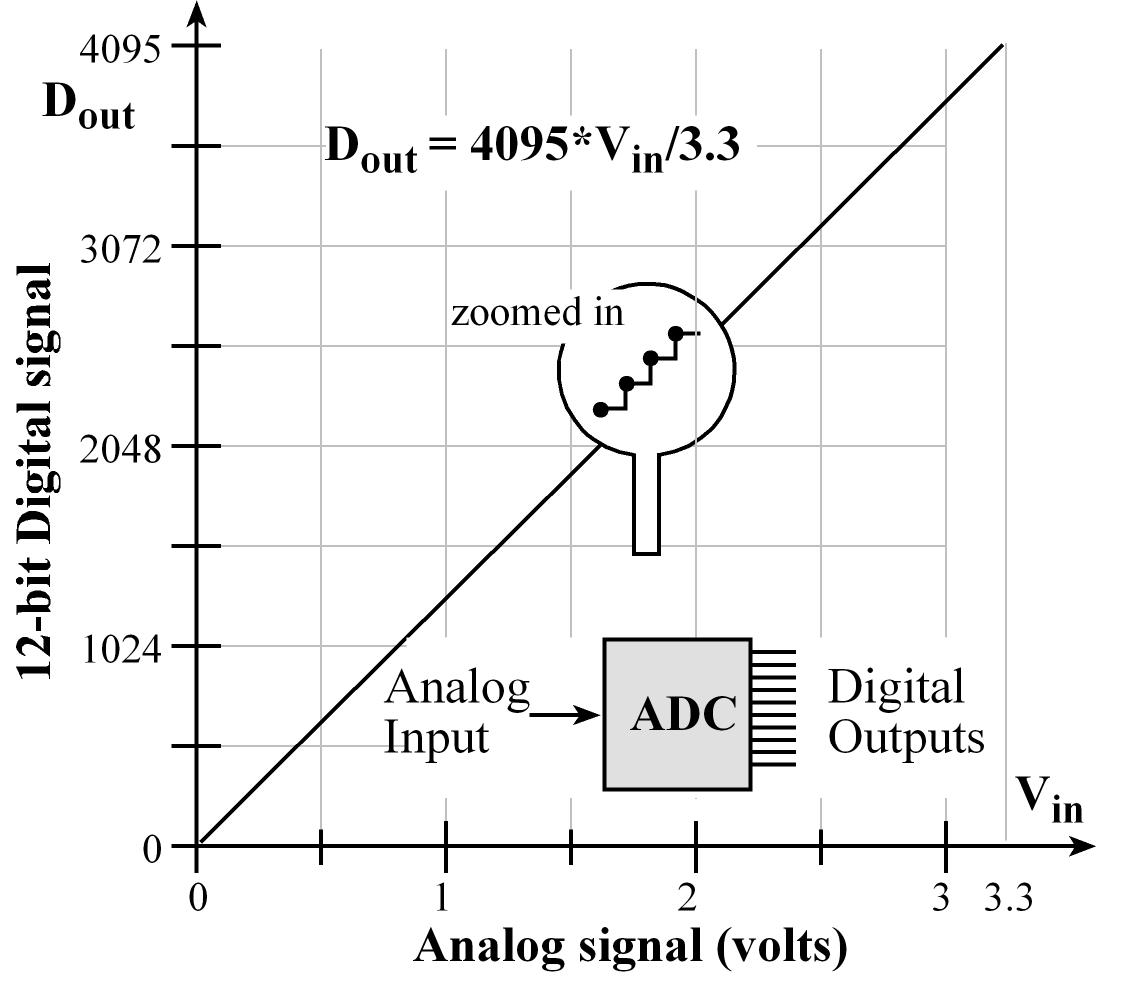
Figure 14.4. A 12-bit ADC converts 0 to 3.3V on its input into a digital number from 0 to 4095.
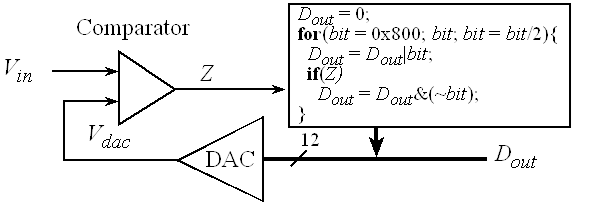
The most pervasive method for ADC conversion is the successive approximation technique, as illustrated in Figure 14.5. A 12-bit successive approximation ADC is clocked 12 times. At each clock another bit is determined, starting with the most significant bit. For each clock, the successive approximation hardware issues a new "guess" on Vdac by setting the bit under test to a "1". If Vdac is now higher than the unknown input, Vin, then the bit under test is cleared. If Vdac is less than Vin, then the bit under test is remains 1. In this description, bit is an unsigned integer that specifies the bit under test. For a 12-bit ADC, bit goes 2048, 1024, 512, 256,...,1. Dout is the ADC digital output, and Z is the binary input that is true if Vdac is greater than Vin.
|
Figure 14.5. A 12-bit successive approximation ADC. |
Video 14.2. Successive Approximation |
This tool allows you
to go through the motions of a ADC sample capture using successive
approximation. It is a game to demonstrate successive approximation.
There is a secret number between 0 to 63 (6-bit ADC) that the computer
has selected. Your job is to learn the secret number by making exactly
6 guesses.
You can guess by entering numbers into the "Enter guess" field and
clicking "Guess". The Tool will tell you if the number you guess is
higher or lower
than the secret number.
When you have the answer, enter it into the "Final answer" field and
click the "Submit answer" button.
The secret number is ???
The secret number is strictly less than these
guesses :
The secret number is greater than or equal to these guesses :
: With successive approximation, what is the strategy when making the first guess? For example, if you had a 10 bit ADC, what would be your first guess?
Observation: The speed of a successive approximation ADC relates linearly with its precision in bits.
Normally we don’t specify accuracy for just the ADC, but rather we give the accuracy of the entire system (including transducer, analog circuit, ADC and software). An ADC is monotonic if it has no missing codes as the analog input slowly rises. This means if the analog signal is a slowly rising voltage, then the digital output will hit all values one at a time, always going up, never going down. The figure of merit of an ADC involves three factors:
- precision (number of bits),
- speed (how fast can we sample), and
- power (how much energy does it take to operate).
How fast we can sample involves both the ADC conversion time (how long it takes to convert), and the bandwidth (what frequency components can be recognized by the ADC). The ADC cost is a function of the number and quality of internal components. Two 12-bit ADCs are built into the TM4C123 microcontroller, called ADC0 and ADC1. You will use ADC0 to collect data and we will use ADC1 and the PD3 pin to implement a voltmeter and oscilloscope using TExaSdisplay.
Table 14.1 shows the ADC0 register bits required to perform sampling on a single channel. Any bits not specified will read 0. There are two ADCs; you will use ADC0 and TExaSdisplay uses ADC1. For more complex configurations refer to the specific data sheet. The value in the ADC0_PC_R specifies the maximum sampling rate, see Table 14.2. This is not the actual sampling rate; it is the maximum possible. Setting ADC0_PC_R to 7, allows the TM4C123 to sample up to 1 million samples per second. The example code in this section will set ADC0_PC_R to 1, because we will be sampling much slower than 125 kHz. It will be more accurate and require less power to run at 125 kHz maximum mode, as compared to 1 MHz maximum mode. In this chapter we will use software trigger mode, so the actual sampling rate is determined by the SysTick periodic interrupt rate; the SysTick ISR will take one ADC sample. On the TM4C123, we will need to set bits in the AMSEL register to activate the analog interface. Furthermore, we will clear bits DEN register to deactivate the digital interface.
|
Address |
31-17 |
16 |
15-3 |
|
2 |
1 0 |
Name |
||
|
0x400F.E638 |
|
|
|
|
ADC1 ADC0 |
SYSCTL_RCGCADC_R |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
31-14 |
13-12 |
11-10 |
9-8 |
7-6 |
5-4 |
3-2 |
1-0 |
|
|
0x4003.8020 |
|
SS3 |
|
SS2 |
|
SS1 |
|
SS0 |
ADC0_SSPRI_R |
|
|
|
|
|
|
|
|
|
|
|
|
|
31-16 |
15-12 |
11-8 |
7-4 |
3-0 |
|
|||
|
0x4003.8014 |
|
EM3 |
EM2 |
EM1 |
EM0 |
ADC0_EMUX_R |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
31-4 |
3 |
2 |
1 |
0 |
|
|||
|
0x4003.8000 |
|
ASEN3 |
ASEN2 |
ASEN1 |
ASEN0 |
ADC0_ACTSS_R |
|||
|
0x4003.8030 |
|
AVE (3 bits) |
ADC0_SAC_R |
||||||
|
0x4003.80A0 |
|
MUX0 |
ADC0_SSMUX3_R |
||||||
|
0x4003.8FC4 |
|
Speed |
ADC0_PC_R |
||||||
|
0x4003.80A4 |
|
TS0 |
IE0 |
END0 |
D0 |
ADC0_SSCTL3_R |
|||
|
0x4003.8028 |
|
SS3 |
SS2 |
SS1 |
SS0 |
ADC0_PSSI_R |
|||
|
0x4003.8004 |
|
INR3 |
INR2 |
INR1 |
INR0 |
ADC0_RIS_R |
|||
|
0x4003.800C |
|
IN3 |
IN2 |
IN1 |
IN0 |
ADC0_ISC_R |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
31-12 |
11-0 |
|
||||||
|
0x4003.80A8 |
|
DATA |
ADC0_SSFIFO3 |
||||||
Table 14.1. The TM4C ADC registers. Each register is 32 bits wide. You will use ADC0 and we will use ADC1 for the grader and to implement the oscilloscope feature.
|
Value |
Description |
|
0x7 |
1M samples/second |
|
0x5 |
500K samples/second |
|
0x3 |
250K samples/second |
|
0x1 |
125K samples/second |
Table 14.2. The maximum sampling rate specified in the ADC0_PC_R register.
Table 14.3 shows which I/O pins on the TM4C123 can be used for ADC analog input channels.
|
IO |
Ain |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
14 |
|
PB4 |
Ain10 |
Port |
|
SSI2Clk |
|
M0PWM2 |
|
|
T1CCP0 |
CAN0Rx |
|
|
|
PB5 |
Ain11 |
Port |
|
SSI2Fss |
|
M0PWM3 |
|
|
T1CCP1 |
CAN0Tx |
|
|
|
PD0 |
Ain7 |
Port |
SSI3Clk |
SSI1Clk |
I2C3SCL |
M0PWM6 |
M1PWM0 |
|
WT2CCP0 |
|
|
|
|
PD1 |
Ain6 |
Port |
SSI3Fss |
SSI1Fss |
I2C3SDA |
M0PWM7 |
M1PWM1 |
|
WT2CCP1 |
|
|
|
|
PD2 |
Ain5 |
Port |
SSI3Rx |
SSI1Rx |
|
M0Fault0 |
|
|
WT3CCP0 |
USB0epen |
|
|
|
PD3 |
Ain4 |
Port |
SSI3Tx |
SSI1Tx |
|
|
|
IDX0 |
WT3CCP1 |
USB0pflt |
|
|
|
PE0 |
Ain3 |
Port |
U7Rx |
|
|
|
|
|
|
|
|
|
|
PE1 |
Ain2 |
Port |
U7Tx |
|
|
|
|
|
|
|
|
|
|
PE2 |
Ain1 |
Port |
|
|
|
|
|
|
|
|
|
|
|
PE3 |
Ain0 |
Port |
|
|
|
|
|
|
|
|
|
|
|
PE4 |
Ain9 |
Port |
U5Rx |
|
I2C2SCL |
M0PWM4 |
M1PWM2 |
|
|
CAN0Rx |
|
|
|
PE5 |
Ain8 |
Port |
U5Tx |
|
I2C2SDA |
M0PWM5 |
M1PWM3 |
|
|
CAN0Tx |
|
|
Table 14.3. Twelve different pins on the TM4C123 can be used to sample analog inputs. The example code will use ADC0 and PE4/Ch9 to sample analog input. TExaSdisplay uses ADC1 and PD3 to implement the oscilloscope feature.
The ADC has four sequencers, but you will use only sequencer 3 in EE319K Labs 8,9,10 (edX MOOC Labs 14 and 15). We set the ADC0_SSPRI_R register to 0x0123 to make sequencer 3 the highest priority. Because we are using just one sequencer, we just need to make sure each sequencer has a unique priority. We set bits 15–12 (EM3) in the ADC0_EMUX_R register to specify how the ADC will be triggered. Table 14.4 shows the various ways to trigger an ADC conversion. More advanced ADC triggering techniques are presented in the book Embedded Systems: Real-Time Interfacing to ARM® Cortex™-M Microcontrollers. However in this chapter, we use software start (EM3=0x0). The software writes an 8 (SS3) to the ADC0_PSSI_R to initiate a conversion on sequencer 3. We can enable and disable the sequencers using the ADC0_ACTSS_R register. There are twelve ADC channels on the TM4C123. Which channel we sample is configured by writing to the ADC0_SSMUX3_R register. The mapping between channel number and the port pin is shown in Table 14.3. For example channel 9 is connected to the pin PE4. The ADC0_SSCTL3_R register specifies the mode of the ADC sample. We set TS0 to measure temperature and clear it to measure the analog voltage on the ADC input pin. We set IE0 so that the INR3 bit is set when the ADC conversion is complete, and clear it when no flags are needed. When using sequencer 3, there is only one sample, so END0 will always be set, signifying this sample is the end of the sequence. In this class, the sequence will be just one ADC conversion. We set the D0 bit to activate differential sampling, such as measuring the analog difference between two ADC pins. In our example, we clear D0 to sample a single-ended analog input. Because we set the IE0 bit, the INR3 flag in the ADC0_RIS_R register will be set when the ADC conversion is complete, We clear the INR3 bit by writing an 8 to the 8 to the ADC0_ISC_R register.
|
Value |
Event |
|
0x0 |
Software start |
|
0x1 |
Analog Comparator 0 |
|
0x2 |
Analog Comparator 1 |
|
0x3 |
Analog Comparator 2 |
|
0x4 |
External (GPIO PB4) |
|
0x5 |
Timer |
|
0x6 |
PWM0 |
|
0x7 |
PWM1 |
|
0x8 |
PWM2 |
|
0x9 |
PWM3 |
|
0xF |
Always (continuously sample) |
Table 14.4. The ADC EM3, EM2, EM1, and EM0 bits in the ADC_EMUX_R register.
We perform the following steps to configure the ADC for software start on one channel. Program 14.1 shows a specific details for sampling PE4, which is channel 9. The function ADC0_InSeq3 will sample PE4 using software start and use busy-wait synchronization to wait for completion.
Step 1. We enable the ADC clock bit 0 in SYSCTL_RCGCADC_R for ADC0.
Step 2. We enable the port clock for the pin that we will be using for the ADC input.
Step 3. We wait for the two clocks to stabilize (some people found extra delay prevented hard faults)
Step 4. Make that pin an input by writing zero to the DIR register.
Step 5. Enable the alternative function on that pin by writing one to the AFSEL register.
Step 6. Disable the digital function on that pin by writing zero to the DEN register.
Step 7. Enable the analog function on that pin by writing one to the AMSEL register.
Step 8. We set the ADC0_PC_R register specify the maximum sampling rate of the ADC. In this example, we will sample slower than 125 kHz, so the maximum sampling rate is set at 125 kHz. This will require less power and produce a longer sampling time, creating a more accurate conversion.
Step 9. We will set the priority of each of the four sequencers. In this case, we are using just one sequencer, so the priorities are irrelevant, except for the fact that no two sequencers should have the same priority.
Step 10. Before configuring the sequencer, we need to disable it. To disable sequencer 3, we write a 0 to bit 3 (ASEN3) in the ADC0_ACTSS_R register. Disabling the sequencer during programming prevents erroneous execution if a trigger event were to occur during the configuration process.
Step 11. We configure the trigger event for the sample sequencer in the ADC0_EMUX_R register. For this example, we write a 0000 to bits 15–12 (EM3) specifying software start mode for sequencer 3.
Step 12. Configure the corresponding input source in the ADC0_SSMUX3 register. In this example, we write the channel number to bits 3–0 in the ADC0_SSMUX3_R register. In this example, we sample channel 9, which is PE4.
Step 13. Configure the sample control bits in the corresponding nibble in the ADC0_SSCTL3 register. When programming the last nibble, ensure that the END bit is set. Failure to set the END bit causes unpredictable behavior. Sequencer 3 has only one sample, so we write a 0110 to the ADC0_SSCTL3_R register. Bit 3 is the TS0 bit, which we clear because we are not measuring temperature. Bit 2 is the IE0 bit, which we set because we want to the RIS bit to be set when the sample is complete. Bit 1 is the END0 bit, which is set because this is the last (and only) sample in the sequence. Bit 0 is the D0 bit, which we clear because we do not wish to use differential mode.
Step 14. Disable interrupts in ADC by clearing bits in the ADC0_IM_R register. Since we are using sequencer 3, we disable SS3 interrupts by clearing bit 3.
Step 15. We enable the sample sequencer logic by writing a 1 to the corresponding ASEN3. To enable sequencer 3, we write a 1 to bit 3 (ASEN3) in the ADC0_ACTSS_R register.
|
void ADC0_InitSWTriggerSeq3_Ch9(void){ Program 14.1. Initialization of the ADC using software start and busy-wait (ADCSWTrigger). |
Video 14.3. ADC Initialization Ritual |
Program 14.2 gives a function that performs an ADC conversion. There are four steps required to perform a software-start conversion. The range is 0 to 3.3V. If the analog input is 0, the digital output will be 0, and if the analog input is 3.3V, the digital output will be 4095.
Digital Sample = (Analog Input (volts) • 4095) / 3.3V(volts)
Step 1. The ADC is started using the software trigger. The channel to sample was specified earlier in the initialization.
Step 2. The function waits for the ADC to complete by polling the RIS register bit 3.
Step 3. The 12-bit digital sample is read out of sequencer 3.
Step 4. The RIS bit is cleared by writing to the ISC register.
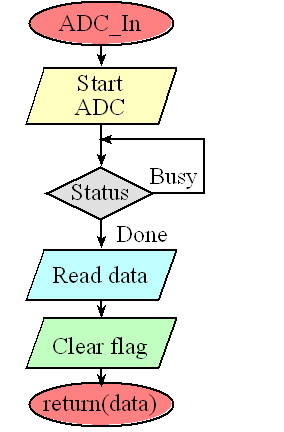
Figure 14.3. The four steps of analog to digital conversion: 1) initiate conversion, 2) wait for the ADC to finish, 3) read the digital result, and 4) clear the completion flag.
|
//------------ADC0_InSeq3------------ // Busy-wait analog to digital conversion // Input: none // Output: 12-bit result of ADC conversion uint32_t ADC0_InSeq3(void){ uint32_t result; ADC0_PSSI_R = 0x0008; // 1) initiate SS3 while((ADC0_RIS_R&0x08)==0){}; // 2) wait for conversion done result = ADC0_SSFIFO3_R&0xFFF; // 3) read result ADC0_ISC_R = 0x0008; // 4) acknowledge completion return result; } Program 14.2. ADC sampling using software start and busy-wait (ADCSWTrigger). |
Video 14.4. Capturing a Sample |
It is important to sample the ADC at a regular rate. One simple way to deploy periodic sampling is to perform the ADC conversion in a periodic ISR. In the following code, the sampling rate is determined by the rate of the periodic interrupt. The global variable, Flag is called a semaphore, which is set when new information is stored into the variable Data. We can connect PF1 to a logic analyzer or oscilloscope to verify the sampling rate.
uint32_t Data; // 0 to 4095
uint32_t Flag; // 1 means new data
void SysTick_Handler(void){
GPIO_PORTF_DATA_R ^= 0x02; // toggle PF1
Data = ADC0_InSeq3(); // Sample ADC
Flag = 1; // Synchronize with other threads
}
There is software in the book Embedded Systems: Real-Time Interfacing to ARM® Cortex™-M Microcontrollers showing you how to configure the ADC to sample a single channel at a periodic rate using a timer trigger. The most time-accurate sampling method is timer-triggered sampling (EM3=0x5).
: If the input voltage is 1.65V, what value will the TM4C 12-bit ADC return?
: If the input voltage is 1.0V, what value will the TM4C 12-bit ADC return?
To collect information from the external world into the computer we must convert it from analog into digital form. This conversion process is called sampling and because the output of the conversion is one digital number at one point in time, there must be a finite time in between conversions, Δt. If we use SysTick periodic interrupts, then this Δt is the time between SysTick interrupts. We define the sampling rate as
fs = 1/Δt
If this information oscillates at frequency f, then according to the Nyquist Theorem, we must sample that signal at
fs > 2f
Furthermore, the Nyquist Theorem states that if the signal is sampled with a frequency of fs, then the digital samples only contain frequency components from 0 to ½ fs. Conversely, if the analog signal does contain frequency components larger than ½ fs, then there will be an aliasing error during the sampling process (performed with a frequency of fs). Aliasing is when the digital signal appears to have a different frequency than the original analog signal.
Discover the
Nyquist Theorem. In this
animation, you control the analog signal by dragging the handle on the
left. Click
and drag the handle up and down to create the analog wave (the blue
continuous wave). The signal is sampled at a fixed rate (fs
=
1Hz) (the red wave). The digital samples are connected by straight red
lines so
you can see the data as captured by the digital samples in the computer.
|
|
Exercise 1: If you move the handle up and down very slowly you will notice the digital representation captures the essence of the analog wave you have created by moving the handle. If you wiggle the handle at a rate slower than ½ fs, the Nyquist Theorem is satisfied and the digital samples faithfully capture the essence of the analog signal.
Exercise 2: However if you wiggle the handle quickly, you will observe the digital representation does not capture the analog wave. More specifically, if you wiggle the handle at a rate faster than ½ fs the Nyquist Theorem is violated causing the digital samples to be fundamentally different from the analog wave. Try wiggling the handle at a fast but constant rate, and you will notice the digital wave also wiggles but at an incorrect frequency. This incorrect frequency is called aliasing.
Figure 14.4 shows what happens when the Nyquist Theorem is violated. In both cases a signal was sampled at 2000 Hz (every 0.5 ms). In the first figure the 200 Hz signal is properly sampled, which means the digital samples accurately describe the analog signal. However, in the second figure, the 2200 Hz signal is not sampled properly, which means the digital samples do not accurately describe the analog signal. This error is called aliasing. Aliasing occurs when the input signal oscillates faster than the sampling rate and it characterized by the digital samples “looking like” it is oscillating at a different rate than the original analog signal. For these two sets of sampled data, notice the digital data are exactly the same.
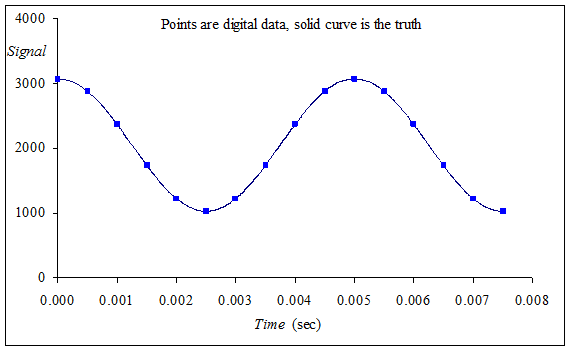
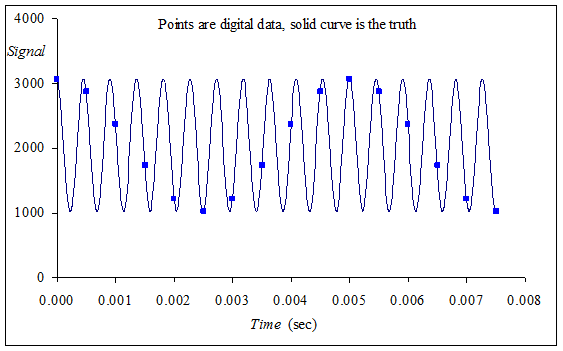
Figure 14.4. Aliasing occurs when the input analog signal oscillates faster than the rate of the ADC sampling.
Video 14.5. Aliasing Demonstration: The Wagon Wheel Effect
: Assume you wish to represent sounds in digital form on the computer, either as inputs sampled from an ADC, or as outputs created with a DAC. The approximate range of canine hearing is 40 to 60 kHz. What sampling rate preverves all information for canine sound?
: The sounds in Lab 10 are sampled at 11 kHz. What range of frequencies can exist in the samples?
: Assume the input is a pure sine wave at 1 kHz, 1.65+1*sin(2*pi*1k*t), and the ADC is sampled at 2 kHz. Will the information be properly represented in the digital data?
Valvano Postulate: If fmax is the largest frequency component of the analog signal, then you must sample more than ten times fmax in order for the reconstructed digital samples to look like the original signal when plotted on a voltage versus time graph.
The resolution of a measurement system is the smallest change in input that can be reliably detected. The accuracy of a measurement system is the average difference between measured value and truth. For most systems, resolution and accuracy are dominated by noise, rather than the precision of the ADC. To improve signal to noise ratio, we can sample the ADC multiple times and average the samples.
Assume the true signal is μ. More formally, μ is the expected value of the signal. When we sample the signal, noise is added, so the
sampled data does not equal the truth. Let x1, x2, x3,... be sampled data on the same true signal. To use the Central Limit Theorem (CLT) we will make the following assumptions:
1) the added noise is independent (the added noise of one sample is not related to the added noise of another sample);
2) the added noise has the same probability distribution (whatever physical process that generated the noise in one sample, creates noise in the other samples);
The CLT states that if you have a signal with mean μ and standard deviation σ and take sufficiently large random samples (n>30), and calculate the average
X = (sum(x1+x2+...+xn))/n
then the distribution of X will be approximately normally distributed (Gaussian). More importantly, the expected value of X will approach μ. If the noise has zero mean (equally likely to be additive as subtractive), then X will approach the true signal as n increases.
One estimate of noise is the standard deviation of multiple samples.
S = sqrt((sum((x1-X)^2+(x2-X)^2+...+(xn-X)^2))/n)
There is a mode on the ADC to automatically take multiple samples and return the average. The ADC0_SAC_R register can be any value from 0 to 6. The possible choices are
ADC0_SAC_R = 0; // take one sample
ADC0_SAC_R = 1; // take 2 samples, return average
ADC0_SAC_R = 2; // take 4 samples, return average
ADC0_SAC_R = 3; // take 8 samples, return average
ADC0_SAC_R = 4; // take 16 samples, return average
ADC0_SAC_R = 5; // take 32 samples, return average
ADC0_SAC_R = 6; // take 64 samples, return average
You will notice the signal to noise ratio will improve dramatically if you use hardware averaging. However, the disadvantage of hardware averaging is the time to convert. If taking one sample takes 8us, then activating 32-point hardware averaging will increase the time to sample to 32*8=128us. Similarly, it will take more electrical power to deploy hardware averaging.
Video . Central Limit Theorem
Because of noise, if we set the ADC input to a constant voltage, and sample it many times, we will get a distribution of digital outputs. We plot the number of times we got an output as a function of the output sample. The shape of this response is called a probability mass function (pmf) characterizing the noise processes. A pmf plots the number of occurrences versus the ADC sample value. To illustrate the CTL, 1.65V was connected to PE2 and the software in Section 14.3 was used to measure the ADC 1000 times. The experiment was performed at three values of ADC0_SAC_R: 0 (1 point), 2 (4-point average), and 4 (16-point average). Notice the shape becomes Gaussian and the standard deviation reduces. In particular, the data with 1 point (no averaging) has two or three humps (not normally distributed), but with 16-point average there is one symmetric hump (normally distributed)
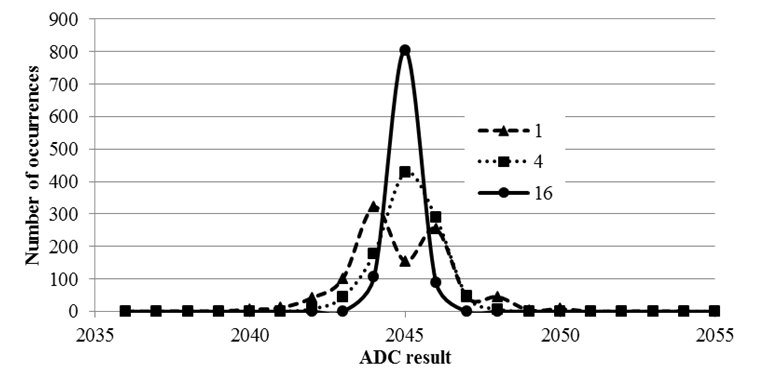
Figure 14.5. Probability mass functions showing hardware averaging improves signal to noise ratio.
: Give an advantage of using hardware averaging.
: Give two disadvantages of using hardware averaging.
: The TM4C123 has hardware averaging. What would you do if you want to deploy averaging, but you are using a different microcontroller that does not support hardware averaging?
In most aspects, running C++ on the microcontroller is identical to running C++ on other machines. However, be aware of the memory limitations of the TM4C123. To run C++ we will create a small heap and continue to have a small stack, knowing that all globals, statics, locals, and heap must fit into the 32 kibibytes of RAM on the TM4C123. The following code exists in the startup file for Lab8_C++ project, creating 1024 bytes of stack and 512 bytes of heap.
Stack_Size EQU 0x00000400
AREA STACK, NOINIT, READWRITE, ALIGN=3
Stack_Mem SPACE Stack_Size
__initial_sp
; Heap Configuration
Heap_Size EQU 0x00000200
AREA HEAP, NOINIT, READWRITE, ALIGN=3
__heap_base
Heap_Mem SPACE Heap_Size
__heap_limit
Video . Running C++ on the TM4C123.
Video . Running a vector.cpp C++ example from EE312H on the TM4C123.
EE319K Lab 8 videos
Educational Objectives of Lab 8
• Sampling
— ADC conversion
— Interrupt-driven periodic sampling
— Calibration and accuracy
— Nyquist Theorem
— Central Limit Theorem
• Thread synchronization
— Mail box
• Fixed-point numbers
— Value = Integer*Constant
• Modular development
• Object oriented design in C++ (EE319H)
Lab8_Introduction
In this video we review the software starter project and overview the design steps for implementing Lab 8. The full scale range of the measurement is determined by the physical size of the potentiometer (some move 0 to 1.5cm, and others move 0 to 2.0cm).
Lab8_SlidePot
We show how to attach slide pot to protoboard. This slide potentiometer has a range of 0 to 2 cm.
Lab8_Calibration
In this video we demonstrate the steps to calibrate the device. We activate hardware averaging to improve signal to noise ratio
Lab8_Accuracy
In this video we demonstrate the steps to determine accuracy of the device. We will also show you how to estimate resolution. We activate hardware averaging to improve signal to noise ratio.
Collect two to five measurements with your distance measurement system. In the left column place the true distances as determined by your eyes looking at the cursor and the ruler. In the right column place the measured distances as determined by your system. When you have entered at least two sets of data, click the "Calculate" button.
True values | Measured values | Errors
The number of data sets is
The maximum error is
The average error is
Lab8_Demo
Demonstration of Lab 8 final solution
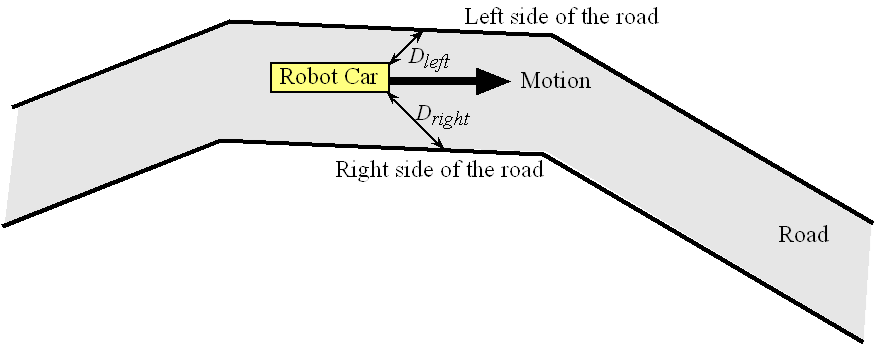
The goal is to drive a robot car autonomously down a road. Autonomous driving is a difficult problem, and we have greatly simplified it and will use this simple problem to illustrate the components of a control system. Every control system has real-world parameters that it wishes to control. These parameters are called state variables. In our system we wish to drive down the middle of the road, so our state variables will be the distance to the left side of the road and the distance to the right side of the road as illustrated in Figure 14.7. When we are in the middle of the road these two distances will be equal. So, let’s define Error as:
Error = Dleft – Dright
If Error is zero we are in the middle of the road, so the controller will attempt to drive the Error parameter to zero.
|
Figure 14.7. Physical layout of the autonomous robot as is drives down the road. |
Video 14.6a. IR Sensor for Robot Car |
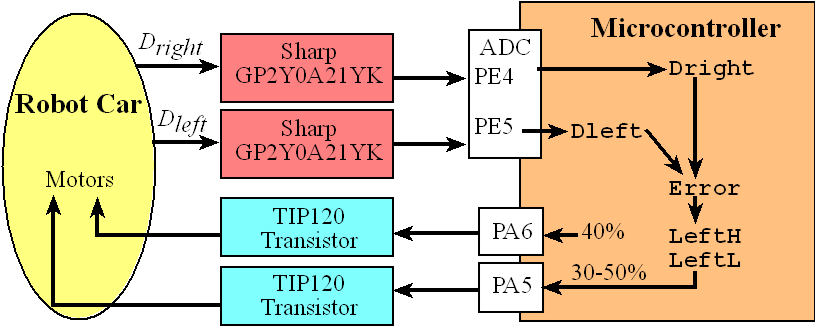
We will need sensors and a data acquisition system to measure Dleft and Dright. In order to simplify the problem we will place pieces of wood to create walls along both sides of the road, and make the road the same width at all places along the track. The Sharp GP2Y0A21YK0F infrared object detector can measure distance (http://www.sharpsma.com) from the robot to the wood. This sensor creates a continuous analog voltage between 0 and +3V that depends inversely on distance to object, see Figure 14.6. We will avoid the 0 to 10 cm range where the sensor has the nonmonotonic behavior. We will use two ADC channels (PE4 and PE5) to convert the two analog voltages to digital numbers. Let Left and Right be the ADC digital samples measured from the two sensors. We can assume distance is linearly related to 1/voltage, we can implement software functions to calculate distance in mm as a function of the ADC sample (0 to 4095). The 241814 constant was found empirically, which means we collected data comparing actual distance to measured ADC values.
Dleft = 241814/Left
Dright = 241814/Right
Figure 14.8 shows the accuracy of this data acquisition system, where the estimated distance, using the above equation, is plotted versus the true distance.
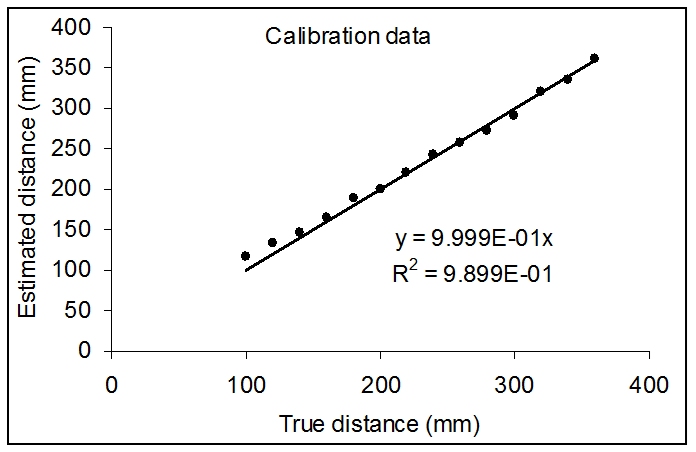
Figure 14.8. Measurement accuracy of the Sharp GP2Y0A21YK0F distance sensor used to measure distance to wall.
Next we need to extend the robot built in Example 12.2. First we build two motor drivers and connect one to each wheel, as shown in Figure 14.9. There will be two PWM outputs: PA6 controls the right motor attached to the right wheel, and PA5 controls the left motor attached to the left wheel. The motors are classified as actuators because they exert force on the world. Similar to Example 12.2 we will write software to create two PWM outputs so we can independently adjust power to each motor. If the friction is constant, the resistance of the motor, R, will be fixed and the power is
Power = (8.42/R)*H/(H+L)
When creating PWM, the period (H+L) is fixed and the duty cycle is varied by changing H. So we see the robot controller changes H, it has a linear effect on delivered power to the motor.
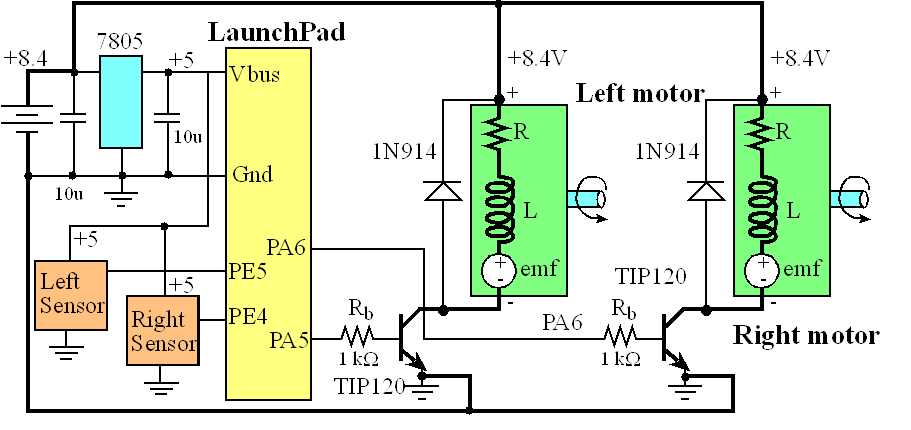
Figure 14.9. Circuit diagram of the robot car. One motor is wire reversed from the other, because to move forward one motor must spin clockwise while the other spins counterclockwise.
The currents can range from 500mA to 1 A, so TIP120 Darlington transistors are used, because they can sink up to 3 A see data sheet. Notice the dark black lines in Figure 14.9; these lines signify the paths of these large currents. Notice also the currents do not pass into or out of the LaunchPad. Figure 14.10 shows the robot car. The two IR sensors are positioned in the front at about 45 degrees.
|
Figure 14.10. Photo of the robot car. |
Video 14.7. Autonomous Robot Demonstration |
Figure 14.11 illustrates the feedback loop of the control system. The state variables are Dleft and Dright. The two sensors create voltages that depend on these two state variables. The ADC samples these two voltages, and software calculates the estimates Dleft and Dright. Error is the difference between Dleft and Dright. The right motor is powered with a constant duty cycle of 40%, while the duty cycle of the left motor is adjusted in an attempt to drive down the middle of the road. We will constrain the duty cycle of the left motor to between 30% and 50%, so it doesn’t over compensate and spin in circles. If the robot is closer to the left wall (Dleft < Dright) the error will be negative and more power will be applied to the left motor, turning it right. Conversely, if the robot is closer to the right wall (Dleft > Dright) the error will be positive and less power will be applied to the left motor, turning it left. Once the robot is in the middle of the road, error will be zero, and power will not be changed. This control algorithm can be written as a set of simple equations. The number “200” is the controller gain and is found by trial and error once the robot is placed on the road. If it is slow to react, then we increase gain. If it reacts too quickly, we decrease the gain.
Error = Dleft - Dright
LeftH = LeftH – 200*Error;
if(LeftH < 30*800) LeftH=30*800; // 30% min
if(LeftH > 50*800) LeftH=50*800; // 50% max
LeftL = 80000 - LeftH; // constant period
Observation: In the field of control systems, a popular approach is called PID control, which stands for proportional integral derivative. The above simple algorithm actually implements the integral term of a PID controller. Furthermore, the two if statements in the control software implement a feature called anti-reset windup.
These controller equations are executed in the SysTick ISR so the controller runs at a periodic rate.
|
Figure 14.11. Block diagram of the closed loop used in the robot car. |
Video 14.6b. The Robot Control System |
Details about microcontroller-based control systems can be found in Chapter 10 of Embedded Systems: Real-Time Operating Systems for ARM® Cortex-M Microcontrollers, 2014, ISBN: 978-1466468863.
Bill of Materials
1) Two DC geared motors, HN-GH12-1640Y,GH35GMB-R, Jameco Part no. 164786
- 0.23in or 6 mm shaft (get hubs to match)
2) Metal or wood for base,
3) Hardware for mounting
- 2 motor mounts 1-1/4 in. PVC Conduit Clamps Model # E977GC-CTN Store SKU # 178931 www.homedepot.com
- some way to attach the LaunchPad (I used an Erector set, but you could use rubber bands)
4) Two wheels and two hubs to match the diameter of the motor shaft
- Shepherd 1-1/4 in. Caster Rubber Wheel Model # 9487 www.homedepot.com
- 2 6mm hubs Dave's Hubs - 6mm Hub Set of Two Part# 0-DWH6MM www.robotmarketplace.com
- 2 3-Inch Diameter Treaded Lite Flite Wheels 2pk Part# 0-DAV5730 www.robotmarketplace.com
5) Two GP2Y0A21YK IR range sensors
- Sparkfun, www.sparkfun.com SEN-00242 or http://www.parallax.com/product/28995
6) Battery
- 8.4V NiMH or 11.1V LiIon. I bought the 8.4V NiMH batteries you see in the video as surplus a long time ago.
I teach a real-time OS class where students write an OS then deploy it on a robot. I have a big pile of these 8.4V batteries,
so I used a couple for the two robots in this class. NiMH are easier to charge,
but I suggest Li-Ion because they store more energy/weight. For my medical instruments,
I use a lot of Tenergy 31003 (7.4V) and Tenergy 31012 (11.1V) (internet search for the best price). You will need a Li-Ion charger.
I have used both of these Tenergy TLP-4000 and Tenergy TB6B chargers.
7) Electronic components
- two TIP120 Darlington NPN transistors
-2 1N914 diodes
-2 10uF tantalum caps
- 7805 regular
-2 10k resistors
Websites to buy robot parts
Robot parts
Pololu Robots and Electronics
Jameco's Robot Store
Robot Marketplace
Sparkfun
Parallax
Tower Hobbies
Surplus parts
Full-service parts
Newark (US) or element14 (worldwide)
Digi-Key
Mouser
Jameco
Part search engine
Reprinted with approval from Embedded Systems:
Introduction to ARM Cortex-M Microcontrollers, 2014, ISBN:
978-1477508992, http://users.ece.utexas.edu/~valvano/arm/outline1.htm
from Embedded Systems: Real-Time
Interfacing to ARM
Cortex-M Microcontrollers, 2014, ISBN: 978-1463590154, http://users.ece.utexas.edu/~valvano/arm/outline.htm
and from Embedded Systems: Real-Time Operating Systems for the ARM Cortex-M Microcontrollers , 2014, ISBN: 978-1466468863, http://users.ece.utexas.edu/~valvano/arm/outline3.htm