Lab 2 Primer

Slides

Sinusoidal generation is a microcosm of real-time DSP systems. Although simple, this task demonstrates many important elements:

• Availability of several algorithms, providing trade offs between runtime implementation complexity and signal quality

• Option to utilize polling, interrupts, or direct memory access (DMA)

• Utilization of floating point computation and conversion

• Utilization of a digital-to-analog converter

• Presence of artifacts due to sampling and quantization

Methods for sinusoidal generation

Given some desired frequency \(f_0\), we want to generate a causal sinusoid

\[x(t) = u(t) \cos (2\pi f_0 t)\]

by sending the discrete signal \(x[n] = u[n] \cos \left( 2\pi \frac{f_0}{f_s} n \right)\) to a digital-to-analog converter (DAC).

We’ll consider four methods to generate this signal:

• Polynomial approximation (GNU math library)

• Difference equation

• Direct Lookup table

• Lookup table with interpolation (ARM DSP math library)

Polynomial approximation (GNU math library)

When the cos function of math.h is invoked, the implementation is system dependent. However, a typical algorithm is to use a polynomial approximation

\[ \cos(t) \approx a_0 + a_1 x + a_2 x^2 + a_3 x^3 \cdots\]

This is the approach used by the GNU scientific library) which stores the first 11 coefficients of the approximation.

Horner’s form is used to minimize the number of operations required

\[ a_{10} x^{10} + a_9 x^9 + a_8 x^8 + \dots + a_0 \]

\[ = ( \dots (((a_{10} x + a_9) x + a_8) x \dots ) + a_0 \]

To generate a sinusoid of frequency \(f_0\), need only repeat a few steps for each sample

1. Calculate \(\cos(\theta)\) via the approximation above and send the value to the DAC

2. Increment \(\theta\) by \(\omega_0 = 2\pi \frac{f_0}{f_s}\)

3. Check if \(\theta\) exceeds \(2\pi\). If it does, subtract \(2\pi\) to prevent overflow or loss of precision.

This method produces a very accurate signal, but requires roughly 20 multiplications and 20 additions per sample in addition to the storage of the coefficients.

It is also extremely flexible, since it allows us to change the frequency as we please by simply changing the the amount at which we increment \(\theta\).

Difference equation

Consider the discrete-time linear time-invariant system governed by the difference equation

\[ y[n] = (2 \cos \omega_0) y[n-1] - y[n-2] + (\sin \omega_0) x[n-1]) \]

This system is particularly interesting when we consider it’s stability. It is on the margin of being bounded-input bounded-output stable, but is technically unstable.

If the system were stable, then the output would eventually decay when excited by an impulse.

For many unstable systems, excitation by an impulse would cause the output to explode to \(\pm \infty\).

However, the impulse response of this particular system is a constant amplitude causal sinusoid, motivating another method for generating a sinusoid:

1. Set the initial conditions to zero and apply a discrete-time impulse as the input.

2. Compute the output \(y[n]\) using the difference equation above.

3. Update the variables corresponding to \(y[n-1]\) and \(y[n-2]\).

4. Repeat from step 2.

This method requires only 2 multiplications and 3 additions per sample and the amount of computation per sample is independent from the desired frequency \(f_0\) and the sampling rate \(f_s\).

Week 2

Lookup table

\(\cos (2\pi f_0 t)\) is a periodic signal with fundamental period \(T_0 = 1/f_0\)

If the ratio \(f_0 / f_s\) is a rational number, it is convenient to express it as \(\frac{f_0}{f_s} = \frac{N}{L}\) where \(N\) and \(L\) are relatively prime. In this case, \(\cos \left( 2\pi \frac{f_0}{f_s} n \right)\) is also periodic with fundamental period \(L\), i.e.,

\[L=\frac{f_s}{\text{gcd}(f_0,f_s)} \text{samples}\]

This means that we can compute the first \(L\) values of the sinusoid ahead of time with arbitrary precision and store them in a lookup table. At runtime, we need only increment the current index and no additional computation is required.

The number \(N\) tells us how many continuous time sinusoidal periods occur during one discrete time period.

Lookup table with interpolation (ARM DSP library)

The ‘arm_cos_f32’ function from the CMSIS DSP library stores a 512 element lookup table regardless of the desired frequency and sampling rate. Like the GNU math library, the function takes a phase as input (in radians), and returns the value of the cosine with that phase using three steps:

1. Find the integer table index \(i\) which is nearest to the desired phase

2. Compute the fractional portion \(p\) of the table index.

3. Return \((1.0-p) \cdot \text{table}[i] + p \cdot \text{table}[i+1]\);

This method requires more memory than the GNU math library but fewer multiply and addition operations.

Since this method always uses the same amount of memory for the lookup table (512 words), it might be preferred to the direct lookup table method if \(L\) is large.

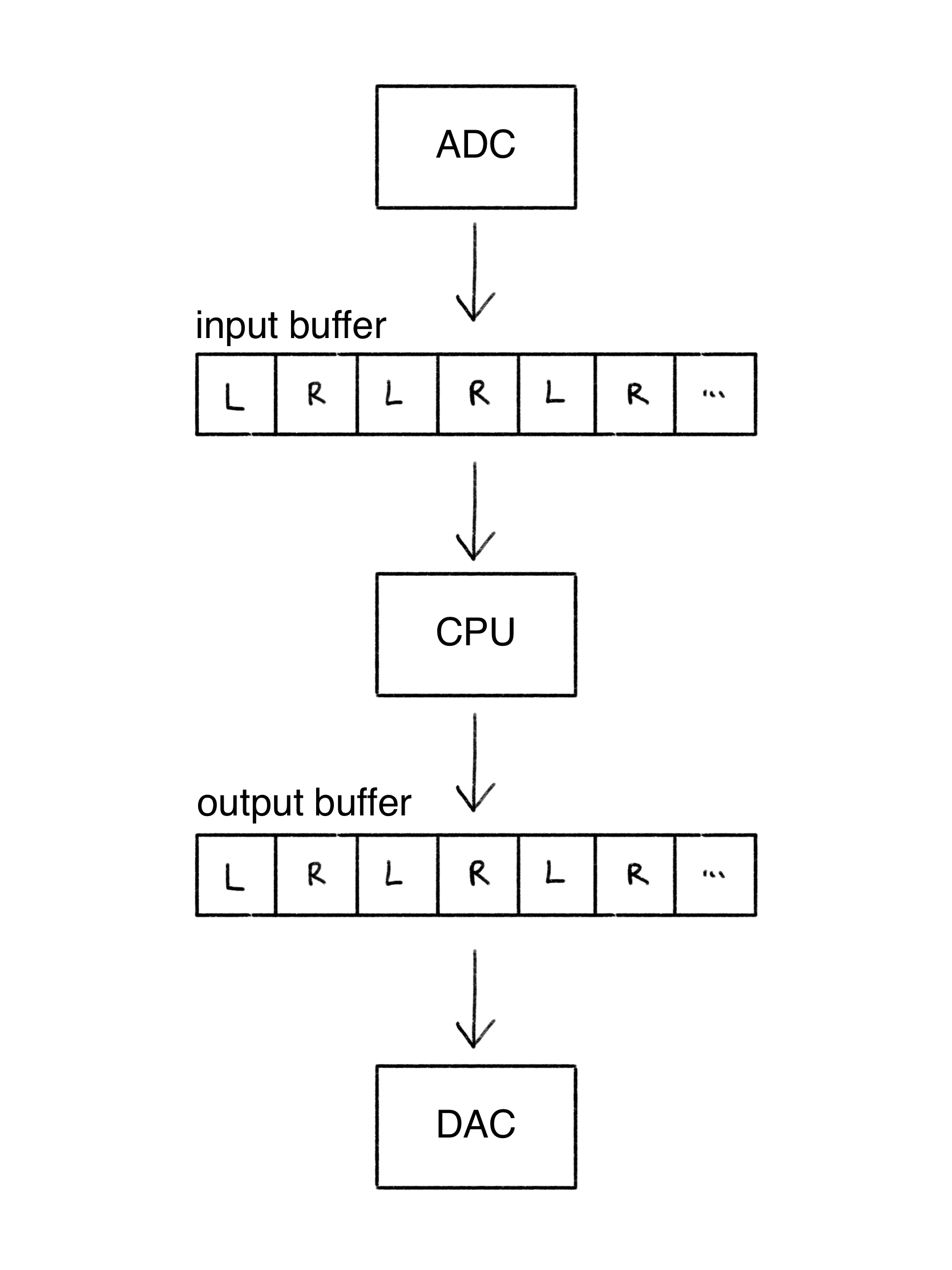
Direct memory access and frame-based processing.

Data is constantly flowing from ADC to main memory and from main memory to DAC. We could move the data using load/store operations, but this would use CPU cycles.

Instead, we can offload this process to a direct memory access (DMA) controller. As samples are generated from an input device (such as an ADC), the DMA controller automatically populates a buffer in CPU addressable memory space.

Rather than process individual samples, we wait for the buffer to fill so that we can process many samples at once. When the buffer is half full, an interrupt is triggered, signaling to the CPU that data is ready to be processed. In the background, samples continue being collected in the second half of the buffer so that no data is ever lost.

After processing is completed, the CPU can stores outputs in a second buffer which is also accessible to the DMA controller. The DMA controller feeds the data to the DAC as needed, avoiding unnecessary CPU load/store operations.

If multiple inputs or outputs are needed (e.g. stereo ADC/DAC), then they are typically interleaved.