
|
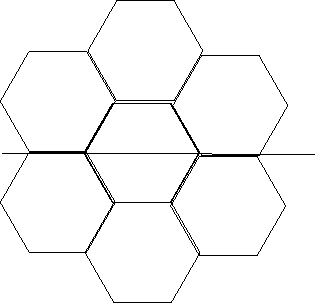
|
 and
and
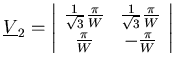
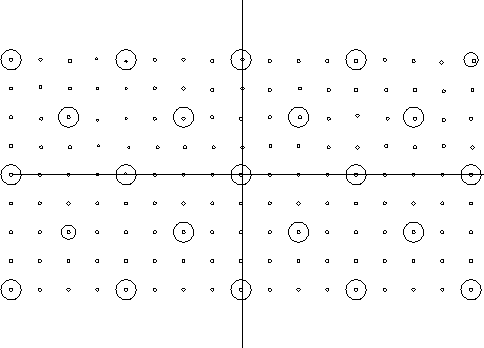 |
- DTFT is not defined.
- LTI systems are difficult to implement on this nonuniform grid.

|

|
 and
and
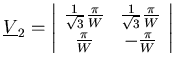
 |
However, periodic deletion of a sample in a block (frame) of samples happens in an communications receiver (such as an ADSL receiver) when the sampling device is sampling faster than the transmitter sampling rate. (The target sampling rate for both transmitter and receiver to use is set by the communication standard.) Similarly, when the sampling device in an communications receiver is sampling slower than the sampling rate being used in the transmitter, the sampling offset accumulates over the block of samples. The accumulation may be great enough so that one fewer sample than expected is in the frame over a fixed time interval. In this case, a sample may have to be inserted at the end of block. If the sampling device were a free-running crystal, then the deletion or insertion of a sample in each block would be periodic. This process of deleting or inserting a sample to align block boundaries in the receiver with that of the transmitter is known as symbol synchronization. Signal analysis and processing would occur one frame at a time.